K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
7 tháng 8 2019
-0,4x2 + 1,2x = 0
⇔ -0,4x.(x – 3) = 0
⇔ x = 0 hoặc x – 3 = 0
+Nếu x – 3 = 0 ⇔ x = 3.
Vậy phương trình có hai nghiệm x = 0 và x = 3.
LM
3
CM
30 tháng 12 2018
a) 3 x 2 + 5x - 1 = 0
Ta có: a = 3; b = 5; c = -1
Δ = b 2 - 4ac = 5 2 - 4.3.(-1) = 37 > 0
Phương trình có 2 nghiệm phân biệt:
Vậy phương trình đã cho có tập nghiệm 
VL
2
4 tháng 3 2021
a) \(4x-9=0\) \(\Leftrightarrow4x=9\) \(\Leftrightarrow x=\dfrac{9}{4}\)
Vậy \(x=\dfrac{9}{4}\)
b) \(-2x+50=0\) \(\Leftrightarrow2x=50\) \(\Leftrightarrow x=25\)
Vậy \(x=25\)
c) \(3x+11=0\) \(\Leftrightarrow3x=-11\) \(\Leftrightarrow x=-\dfrac{11}{3}\)
Vậy \(x=-\dfrac{11}{3}\)
CM
7 tháng 4 2018
Phương trình 159x2 – 2x – 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x1; x2.
Theo hệ thức Vi-et ta có: 
VL
1
VL
1
17 tháng 1 2021
a) Ta có: \(2x^2-3x-2=0\)
nên a=2; b=-3 và c=-2
Vì \(x_1\) và \(x_2\) là nghiệm của phương trình \(2x^2-3x-2=0\) nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{3}{2}\\x_1\cdot x_2=-\dfrac{2}{2}=-1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=-1\)
nên \(2\cdot x_1\cdot x_2=-2\)
Ta có: \(\left(x_1+x_2\right)^2=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2+2\cdot x_1\cdot x_2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2=\dfrac{9}{4}+2=\dfrac{17}{4}\)
PT
1
CM
13 tháng 3 2018
b) x 4 - 5 x 2 + 4 = 0
Đặt t = x 2 ≥ 0 , ta có phương trình:
t 2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t 1 = 1 (nhận) ; t 2 = 4 (nhận)
với t = 1 ⇔ x 2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x 2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
0,4x2 + 1 = 0
⇔ 0,4x2 = -1
⇔
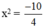
Phương trình vô nghiệm vì x2 ≥ 0 với mọi x.