
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


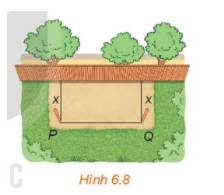
a) Theo bài ra ta có: \(x + x + PQ = 20 \Rightarrow PQ = 20 - 2x\)(m)
b) Diện tích của mảnh đất được rào chắn là: \(\)\(x.PQ = x.(20 - 2x) = - 2{x^2} + 20x({m^2})\)

Ta có: \(B = \){Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
và H = {Hương; Hiền; Hân}
Vậy các phần tử của H đều là phần tử của tập hợp B.

Kí hiệu H là tập hợp tất cả các thành viên tham gia chuyên đề 1 hoặc chuyên đề 2.
Tập hợp các bạn tham gia chuyên đề 1: A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
Tập hợp các bạn tham gia chuyên đề 2: B = {Hương; Chi; Tú; Khánh; Bình; Hân; Hiền; Lam}
Vậy H = {Nam; Ngân; Hân; Hiền; Lam; Khánh; Bình; Hương; Chi; Tú }
Chú ý khi giải
Mỗi phần tử chỉ liệt kê một lần.

A= {Nam; Hương; Chi; Tú; Bình; Ngân; Khánh}
X = {Khánh; Bình; Hương; Chi; Tú }
Có Nam và Ngân chỉ tham gia chuyên đề 1.
Tập hợp các thành viên chỉ tham gia Chuyên đề 1 mà không tham gia Chuyên đề 2 là
G = {Nam; Ngân}

- Lập hệ:
Do số lượng máy nhập vào phải là số tự nhiên nên ta có \(x \ge 0,y \ge 0\).
Từ HĐ 1 ta có hai bất phương trình là \(x + y \le 100\) và \(2x + y \le 120\)
Vậy hệ bất phương trình từ HĐ 1 là
\(\left\{ \begin{array}{l}x + y \le 100\\2x + y \le 120\\x \ge 0\\y \ge 0\end{array} \right.\).
Cặp số (x;y)=(50;10) là một nghiệm của hệ BPT vì thay x= 50, y= 10 ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{50 + 10 \le 100}\, \text {(Đúng)}\\
{2.50 + 10 \le 120}\, \text {(Đúng)}\\
{50 \ge 0}\, \text {(Đúng)}\\
{10 \ge 0}\, \text {(Đúng)}
\end{array}} \right.\)

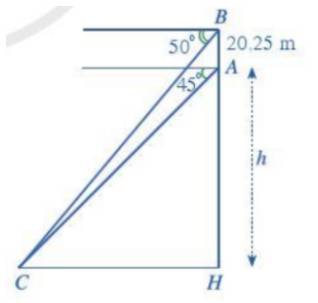
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)
Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)
Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)
\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)
Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.

Các con vật xuất hiện trong hình vẽ là: Voi, ngựa, vượn, chó, mèo, chuột
a) Câu “Có 6 con vật xuất hiện trong hình vẽ” của Khoa là đúng.
b) Câu “Có 5 con vật xuất hiện trong hình vẽ” của An là sai.
c) Câu “Có bao nhiêu con vật xuất hiện trong hình vẽ?” là câu hỏi, không xác định được tính đúng sai.

Ta có: \(\left| {8848,86 - 8848} \right| = 0,86\)
\(\left| {8848,86 - 8848,13} \right| = 0,73\)
\(\left| {8848,86 - 8844,43} \right| = 4,43\)
\(\left| {8848,86 - 8850} \right| = 1,14\)
Trong các số 0,86; 0,73; 4,43; 1,14 thì số 0,73 là số nhỏ nhất.
Do đó trong các số 8 848 m; 8 848,13 m; 8 844,43 m; 8 850 m thì số ; 8 848,13 m là số gần nhất với số được công bố ngày 8-12-2020.
Chú ý
Giá trị tuyệt đối |a-b| càng nhỏ thì a và b càng gần nhau.

Sau khi xuất phát được 2 giờ tức là máy bay đi được \(\frac{2}{3}\) quãng đường thì ta có máy bay ở điểm M hay là ta có \(\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} \)
Tọa độ vectơ \(\overrightarrow {AB} = \left( { - 300;400} \right) \Rightarrow \overrightarrow {AM} = \left( { - 200;\frac{{800}}{3}} \right) \Rightarrow \overrightarrow {OM} = \overrightarrow {AM} - \overrightarrow {AO} = \left( { - 600;\frac{{650}}{3}} \right)\)
Vậy tọa độ máy bay sau 2 giờ xuất phát là: \(\left( { - 600;\frac{{650}}{3}} \right)\)


Ta có \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega \right)}} = \frac{1}{{C_{45}^6}} = \frac{1}{{8145060}}\) và \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega \right)}} = \frac{{234}}{{C_{45}^6}} = \frac{{39}}{{1357510}}\).