Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi x (km/h) là vận tốc của bè gỗ. Điều kiện: x > 0
Khi đó vận tốc của xuồng máy là x + 12 (km/h)
thời gian bè từ lúc trôi đến lúc gặp xuồng là 20/x (giờ)
thời gian xuồng từ lúc đi đến lúc gặp bè là 20/(x + 12) (giờ)
Bè gỗ trôi trước xuồng máy 5 giờ 20 phút = 5.(1/3) (giờ) = 16/3 (giờ)
Theo đề bài, ta có phương trình:
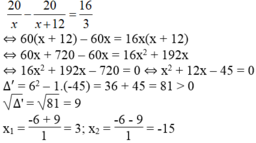
Giá trị x = -15 không thỏa mãn điều kiện bài toán.
Vậy vận tốc trôi của bè gỗ là 3km/h

Gọi vận tốc bè gỗ là v1 (km/h) (v1 > 0)
=> Vận tốc thuyền : v1 + 4 km/h (v1 + 4 > 0)
Đổi : 3 giờ 20 phút = 10/3 giờ
Ta có v1.10/3 + v1.\(\frac{10}{v_1+4}\) = (v1 + 4).\(\frac{10}{v_1+4}\) (= 10)
=> v1.10/3 + v1.\(\frac{10}{v_1+4}\) = v1.\(\frac{10}{v_1+4}\)+ 4\(\frac{10}{v_1+4}\)
=> \(\frac{v_1.10}{3}=\frac{40}{v_1+4}\)
=> 3.40 = (v1+ 4).v1.10
=> (v1 + 4).v1 = 12
=> (v1)2 + 4.v1 - 12 = 0
=> (v1 + 2)(v1 - 6) = 0
=> \(\orbr{\begin{cases}v_1+2=0\\v_1-6=0\end{cases}}\Rightarrow\orbr{\begin{cases}v_1=-2\left(\text{loại}\right)\\v_1=6\left(tm\right)\end{cases}}\)
Vậy vận tốc của bè là 6km/h

Một tên nhà giàu keo kiệt thuê người đào giếng . Người thợ đòi tiền công 100 đồng , tên nhà giàu không bằng lòng vì chê đắt quá . Người thợ bèn nói : " Thế thì tính như sau : 1m đầu trả 1 đồng , 1m thứ hai trả 2 đồng , 1m thứ ba trả 4 đồng , 1m thứ tư trả 8 đồng ,..., cứ trả như thế cho đến khi xong việc " . Tên nhà giàu nghĩ là quá rẻ nên bằng lòng ngay . Hãy nghĩ xem tên nhà giàu phải trả bao nhiêu tiền công khi giếng đào sâu tới 10m ?
Ta thấy :
Đào 1 m : Trả 1 đồng
Đào 2 m : Trả 1 x 2 = 2 đồng
Đào 3 m : Trả 1 x 2 x 3 = 6 đồng
.....................................................
Đào 10 m : Trả 1 x 2 x 2 x ... x 2 = 512 đồng ( có 9 thừa số 2 )
Số tiền cần trả :
1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 + 256 + 512 = 1023 đồng

Lời giải:
Gọi vận tốc cano khi nước yên lặng là $a$ km/h. Vận tốc cano lúc xuôi dòng là $a+4$ km/h, lúc ngược dòng là $a-4$ km/h
Thời gian cano đi quãng đường AB dài $24$ km rồi quay trở lại gặp bè gỗ tại điểm $C$ cách $A$ $8$ km là:
$\frac{AB}{v_{x}}+\frac{CB}{v_n}=\frac{24}{a+4}+\frac{24-8}{a-4}$ (h)
Thời gian này cũng chính là thời gian bè gỗ đi tới $C$.
Do đó:
$\frac{24}{a+4}+\frac{16}{a-4}=\frac{8}{4}=2$
$\Rightarrow a=20$ (km) (nhận) hoặc $a=0$ (km) (loại)
Vậy ............

Gọi vận tốc riêng của cano là x (km/h) và vận tốc riêng của dòng nước là y (km/h) với x>y>0
Vận tốc cano khi xuôi dòng: \(x+y\) (km/h)
Vận tốc cano khi ngược dòng: \(x-y\) (km/h)
Thời gian cano đi xuôi dòng 96km là: \(\dfrac{96}{x+y}\) giờ
Thời gian cano đi ngược dòng: \(\dfrac{96}{x-y}\) giờ
Do cano đi xuôi dòng và ngược dòng về A hết 14 giờ nên ta có pt:
\(\dfrac{96}{x+y}+\dfrac{96}{x-y}=14\)
Thời gian cano ngược dòng đến khi gặp bè nứa: \(\dfrac{96-24}{x-y}=\dfrac{72}{x-y}\) giờ
Thời gian bè nứa xuôi dòng đến khi gặp cano: \(\dfrac{24}{y}\) giờ
Ta có pt: \(\dfrac{72}{x-y}=\dfrac{24}{y}\Rightarrow x=4y\)
Ta được hệ: \(\left\{{}\begin{matrix}\dfrac{96}{x+y}+\dfrac{96}{x-y}=14\\x=3y\end{matrix}\right.\)
Thế pt dưới vào pt trên:
\(\dfrac{96}{4y}+\dfrac{96}{2y}=14\)
\(\Leftrightarrow\dfrac{72}{y}=14\)
\(\Rightarrow y=\dfrac{36}{7}\)
\(\Rightarrow x=\dfrac{108}{7}\)

đổi: 6h15'=25/4
gọi vận tốc bè : x( km/h; x>0)
=> vận tốc của xuồng máy: x+10 (kmh) => vận tốc xuôi dòng: x+10+x=2x+10
thời gian xuồng đến chỗ gặp: 15/2x+10.
thời gian bè đến chỗ gặp: 15/x
vì bè đi trước 25/4 h nên ta có pt:
\(\frac{15}{x}-\frac{15}{x+10}=\frac{25}{4}\Leftrightarrow\frac{15x+150-15x}{x^2+10x}=\frac{25}{4}\Rightarrow600=25x^2+250x\Leftrightarrow x^2+10x-24=0\Leftrightarrow\left(x-2\right)\left(x+12\right)=0\)
=> x=2(t/m) hoặc x=-12(l)
=> vận tốc của bè gỗ là: 2 km/h