Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cam là x, số quýt là y (x, y ∈ N* ; x < 17, y < 17).
Quýt, cam 17 quả tươi ⇒ x + y = 17.
Mỗi quả quýt chia ba ⇒ Có 3y miếng quýt
Chia mười mỗi quả cam ⇒ Có 10x miếng cam
Tổng số miếng tròn 100 ⇒ 10x + 3y = 100.
Ta có hệ phương trình:
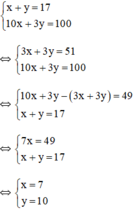
Vậy có 7 quả cam và 10 quả quýt.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình:
Bước 1: Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2: Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3: Đối chiếu nghiệm với điều kiện và kết luận.

Gọi số cam là x ( quả )
số quýt là y (quả)
Điều kiện x, y > 0
Theo đề bài ta có hệ phương trình :
\(\left\{{}\begin{matrix}x+y=7\left(1\right)\\10x+3y=100\left(2\right)\end{matrix}\right.\)
(1) ⇔ y = 17 - x (3)
Thế (3) vào (2): 10x + 3(17 - x) = 100
⇔ 10x + 51 - 3x = 100 ⇔ 7x = 49 ⇔ x = 7
Từ đó y = 17 - 7 = 10
Vậy có 7 quả cam và 10 quả quýt.

Gọi số cam là x, số quýt là y. Điều kiện x, y là số nguyên dương.
Vậy có 7 quả cam và 10 quả quýt.
Gọi số quýt là x , số cam là y ( x ; y khác 0 )
Theo bài ra ta có :
\(x+y=17\)
\(\Rightarrow3\left(x+y\right)=51\left(1\right)\)
\(3x+10y=100\)
\(\Rightarrow3\left(x+y\right)+7y=100\left(2\right)\)
Lấy \(\left(2\right)-\left(1\right)\); ta được :
\(7y=100-51\)
\(\Rightarrow7y=49\)
\(\Rightarrow y=7\)
Mà \(x+y=17\)
\(\Rightarrow x=17-7=10\)
Vậy số quýt là 10 quả ; số cam là 7 quả

Gọi x là số quýt (0<x<17)
Gọi y là số cam (0<y<17)
Theo đề bài ta có hệ pt:
{x+y=17
{3x+10y=100
Tự Tính
<=> {x=10
{y=7
Vậy số quýt là 10 quả ;cam là 7 quả
mình chỉ biết câu này thôi

Gọi số cam là x, số quýt là y. Điều kiện x,y là số nguyên dương.
Quýt ,cam mười bảy quả tươi nên ta có tổng số quả: x+y=17
Chia ba mỗi quả quýt rồi nên số miếng quýt là: 3y (miếng)
Còn cam mỗi quả chia mười vừa xinh nên số miếng cam là: 10x (miếng)
Trăm người , trăm miếng ngọt lành, vậy ta có: 10x+3y=100
Từ đó ta có hệ:
{x+y=1710x+3y=100⇔{3x+3y=5110x+3y=100
⇔{−7x=−4910x+3y=100⇔{x=73y=100−10x
⇔{x=73y=100−10.7⇔{x=7y=10(thỏa mãn)
Vậy có 10 quả quýt và 7 quả cam.
Giải :
Giả sử 17 quả đều là quýt thì có số phần là :
17 x 3 = 51 ( phần )
Số phần giảm đi là :
100 - 51 = 49 ( phần )
Số cam là :
49 : 7 = 7 ( quả )
Số quýt là
17 - 7 = 10 ( quả )

bài tập 2:(bài toán cổ)
Quýt ngon mỗi quả chia ba
Cam ngon mỗi quả chia ra làm mười
Mỗi người một miếng, trăm người
Có mười bẩy quả, chia rồi còn đâu!
Hỏi có mấy quả cam, mấy quả quýt?
(Trả lời: 7 quả cam, 10 quả quýt!)

Bài 28
Đặt sô cần tìm là a và b (a>b)
ta có a+b=1006=> a=1006-b
a=b*2+124=> 1006-b= b*2 +124 => b= 294=> a= 712
bài 29
Gọi số cam là a
số quýt là b
ta có a+b=17=> a=17-b
3*b+a*10=100
=> 3*b+10*(17-b) = 100 => b=10=> a=7
Bài 28:
Gọi số lớn là x, số nhỏ là y (a, y ∈ N*); x > 124. Ta có: Tổng bằng 1006 nên được: x + y = 1006
Số lớn chia số nhỏ được thương là 2, số dư là 124 nên ta có điều kiện là y > 124 và có phương trình: x = 2y + 124
Ta có HPT:
\(\hept{\begin{cases}x+y=1006\\x=2y+124\end{cases}\Leftrightarrow\hept{\begin{cases}x+y=1006\\x-2y=124\end{cases}}}\)
Vậy hai số tự nhiên phải tìm là 712 và 294.
Bài 29:
Gọi số cam là x, số quýt là y. Điều kiện x, y là số nguyên dương.
Theo đề bài, ta có HPT: \(\hept{\begin{cases}x+y=17\left(1\right)\\10x+3y=100\left(2\right)\end{cases}}\)
\(\text{PT}\left(1\right)\Leftrightarrow y=17-x\)
Thế (3) vào (2): 10x + 3(17 - x) = 100
<=> 10x + 51 - 3x = 100 <=> 7x = 49 <=> x = 7
=> y = 17 - 7 = 10
=> Có 7 quả cam và 10 quả quýt.
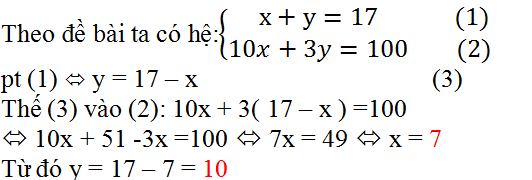
Gọi số cam là x, số quýt là y (x, y ∈ N* ; x < 17, y < 17).
Quýt, cam 17 quả tươi ⇒ x + y = 17.
Mỗi quả quýt chia ba ⇒ Có 3y miếng quýt
Chia mười mỗi quả cam ⇒ Có 10x miếng cam
Tổng số miếng tròn 100 ⇒ 10x + 3y = 100.
Ta có hệ phương trình:
Vậy có 7 quả cam và 10 quả quýt.