Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pt 1: 4(1/a + 1/b )= 1
Pt 2: 1/a + 3/b = 5/12
Từ 2 pt ta được hpt sau đó giải a,b với a là t/g người t1 làm cv đó, b là t/g người t2 làm cv đó

Đáp án A
Gọi thời gian người thợ thứ nhất làm một mình xong việc là x(giờ) (x > 16)
Thời gian người thợ thứ hai làm một mình xong việc là y(giờ) (y > 16)
Suy ra trong thời gian 1 giờ người thợ thứ nhất làm được 1/x công việc
Trong thời gian 3 giờ người thợ thứ nhất làm được 3/x công việc
Trong thời gian 1 giờ người thợ thứ hai làm được 1/y công việc
Trong thời gian 6 giờ người thợ thứ hai làm được 6/y công việc
Hai người cùng làm trong 16 giờ thì xong việc, nên 1 giờ cả 2 người làm được 1/16 ta có phương trình:
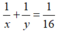
Người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì được một phần tư công việc, ta có phương trình:
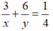
Từ đó ta có hệ phương trình:
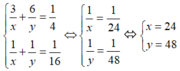
Kết luận: thời gian người thợ thứ nhất làm một mình xong việc là 24 (giờ)
Thời gian người thợ thứ hai làm một mình xong việc là 48 giờ

Cả 2 người thợ làm cùng nhau mỗi giờ làm được
\(\dfrac{1}{4}+\dfrac{1}{6}=\dfrac{5}{12}\)( Công việc )
Cả 2 người thợ làm chung thì hoàn thành công việc sau
\(1:\dfrac{5}{12}=\dfrac{12}{5}=24h\)
Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x,y
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{4}{x}+\dfrac{6}{y}=\dfrac{5}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{24}\\\dfrac{1}{y}=\dfrac{1}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=24\end{matrix}\right.\)

Gọi thời gian người 1 làm một mình là x (h)
Thời gian người 2 làm một mình là y(h)
Đk : x;y > 18
1 giờ người 1 làm được 1 : x = 1/x công việc
1 giờ người 2 làm được 1 : y = 1/y công việc
=> 1 giờ 2 người làm được : \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\)(1)
Lại có : Sau 14h 2 người làm riêng thì 2 người làm được
\(\dfrac{6}{x}+\dfrac{8}{y}=\dfrac{2}{5}\)(2)
Từ (1) và (2) => HPT : \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{6}{x}+\dfrac{8}{y}=\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{1}{6}\\\dfrac{3}{x}+\dfrac{4}{y}=\dfrac{1}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{y}=\dfrac{1}{30}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}y=30\\x=45\end{matrix}\right.\)(tm)
Vậy ...

gọi x là thời gian người thứ 2 làm việc (x;y>8)
y là thời gian người thứ nhất làm việc
theo đề bài ta có hệ phương trình
\(\hept{\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{8}\\\frac{8}{x}+\frac{2}{y}=\frac{1}{2}\end{cases}}\)
đặt \(\frac{1}{x}\)là u; \(\frac{1}{y}\)là v ta có
\(\hept{\begin{cases}u+v=\frac{1}{8}\\8u+2v=\frac{1}{2}\end{cases}}\)<=> u=\(\frac{1}{24}\)=> x=24
vậy thời gian người thứ 2 làm 1 mình tring 24h thì xong công việc

Gọi x là số ngày của người 1 làm 1 mình xong việc
y là số ngày của người 2 làm 1 mình xong việc
ĐK: x;y > 0
Số việc người 1 làm trong 1h là \(\frac{1}{x}\)
Số việc người 2 làm trong 1h là \(\frac{1}{y}\)
Theo đề bài ta có hệ phương trình:
\(\hept{\begin{cases}4\left(\frac{1}{x}+\frac{1}{y}\right)=1\\10.\frac{1}{x}+\frac{1}{y}=1\end{cases}}\)
Từ đó bạn giải hệ và kết luận.

Làm lại qua đây vậy:
Gọi số ngày người thứ nhất làm một mình xong việc là x
số ngày người thứ hai làm một mình xong việc là y
ĐK: x;y > 0
Số việc người thứ nhất làm trong 1h là: \(\frac{1}{x}\)
Số việc người thứ hai làm trong 1h là: \(\frac{1}{y}\)
Theo đề bài ta có hệ phương trình:
\(\hept{\begin{cases}4\left(\frac{1}{x}+\frac{1}{y}\right)=1\\10.\frac{1}{x}+\frac{1}{y}=1\end{cases}}\)
Từ đây bạn giải tiếp & kết luận. Không hiểu hỏi nha hiccc
Gọi thời gian làm xong việc một mình của người thứ nhất và người thứ hai lần lượt là \(x,y\left(x,y>0\right)\)(đơn vị: h)
Trong 1 giờ, người thứ nhất làm xong \(\frac{1}{x}\)công việc còn người thứ hai làm xong \(\frac{1}{y}\)công việc.
2 người cùng làm trong 12 giờ thì xong công việc nên ta có phương trình \(\frac{12}{x}+\frac{12}{y}=1\)(1)
Trong 8 giờ, 2 người hoàn thành \(\frac{8}{x}+\frac{8}{y}\)công việc, sau đó người thứ 2 làm việc một mình trong 6h40p \(=\frac{20}{3}\)h, tức là hoàn thành thêm \(\frac{20}{3y}\) công việc thì xong công việc nên ta có pt \(\frac{8}{x}+\frac{8}{y}+\frac{20}{3y}=1\)(2)
Từ (1) và (2) ta có hpt \(\hept{\begin{cases}\frac{12}{x}+\frac{12}{y}=1\\\frac{8}{x}+\frac{8}{y}+\frac{20}{3y}=1\end{cases}}\)
Đặt \(\hept{\begin{cases}\frac{1}{x}=a\left(a>0\right)\\\frac{1}{y}=b\left(b>0\right)\end{cases}}\), hpt trên trở thành \(\hept{\begin{cases}12a+12b=1\\8a+8b+\frac{20}{3}b=1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}24a+24b=2\\24a+24b+20b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}12a+12b=1\\20b=1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}12a+12.\frac{1}{20}=1\\b=\frac{1}{20}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}a=\frac{1}{30}\\b=\frac{1}{20}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{30}\\\frac{1}{y}=\frac{1}{20}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=30\\y=20\end{cases}}\)(nhận)
Vậy người thứ nhất làm một mình xong công việc mất 30h, người thứ hai làm xong công việc một mình mất 20h