Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt A'B'=a
ΔA'B'C' vuông tại B'
=>\(\left(A^{\prime}B^{\prime}\right)^2+\left(B^{\prime}C^{\prime}\right)^2=\left(A^{\prime}C^{\prime}\right)^2\)
=>\(\left(A^{\prime}C^{\prime}\right)^2=a^2+a^2=2a^2\)
=>\(A^{\prime}C^{\prime}=a\sqrt2\) (1)
Vì ABCD.A'B'C'D' là hình lập phương
nên A'A//C'C và A'A=C'C
=>A'ACC' là hình bình hành
=>A'C'//AC
=>\(\hat{AC;A^{\prime}D}=\hat{A^{\prime}C^{\prime};A^{\prime}D}=\hat{DA^{\prime}C^{\prime}}\)
A'B'C'D' là hình vuông
=>A'D'=D'C'=C'B'=A'B'=a
Vì ABCD.A'B'C'D' là hình lập phương
nên A'B'BA là hình vuông
=>A'A=A'B'=a
Vì ABCD.A'B'C'D' là hình lập phương
nên D'D=A'A=a
ΔA'D'D vuông tại D'
=>\(\left(D^{\prime}A^{\prime}\right)^2+\left(D^{\prime}D\right)^2=\left(A^{\prime}D\right)^2\)
=>\(\left(A^{\prime}D\right)^2=a^2+a^2=2a^2\)
=>\(A^{\prime}D=a\sqrt2\)
D'C'CD là hình vuông
=>\(\left(DC^{\prime}\right)^2=\left(D^{\prime}D\right)^2+\left(D^{\prime}C^{\prime}\right)^2=a^2+a^2=2a^2\)
=>\(DC^{\prime}=a\sqrt2\)
=>DC'=DA'=A'C'
=>ΔDA'C' đều
=>\(\hat{DA^{\prime}C^{\prime}}=60^0\)
=>\(\hat{AC;A^{\prime}D}=60^0\)
=>Chọn C

Câu 1: \(\frac{\pi}{2}<\alpha,\beta<\pi\)
=>\(\sin\alpha>0;\sin\beta>0;cos\alpha<0;cos\beta<0\)
\(\sin^2\alpha+cos^2\alpha=1\)
=>\(cos^2\alpha=1-\sin^2\alpha=1-\left(\frac13\right)^2=\frac89\)
mà \(cos\alpha<0\)
nên \(cos\alpha=-\frac{2\sqrt2}{3}\)
Ta có: \(\sin^2\beta+cos^2\beta=1\)
=>\(\sin^2\beta=1-\left(-\frac23\right)^2=1-\frac49=\frac59\)
mà \(\sin\beta>0\)
nên \(\sin\beta=\frac{\sqrt5}{3}\)
\(\sin\left(\alpha+\beta\right)=\sin\alpha\cdot cos\beta+cos\alpha\cdot\sin\beta\)
\(=\frac13\cdot\frac{-2}{3}+\frac{-2\sqrt2}{3}\cdot\frac{\sqrt5}{3}=\frac{-\sqrt2-2\sqrt{10}}{9}\)
Câu 2:
\(P=cos\left(a+b\right)\cdot cos\left(a-b\right)\)
\(=\frac12\cdot\left\lbrack cos\left(a+b+a-b\right)+cos\left(a+b-a+b\right)\right\rbrack=\frac12\cdot\left\lbrack cos2a+cos2b\right\rbrack\)
\(=\frac12\cdot\left\lbrack2\cdot cos^2a-1+2\cdot cos^2b-1\right\rbrack=cos^2a+cos^2b-1\)
\(=\left(\frac13\right)^2+\left(\frac14\right)^2-1=\frac19+\frac{1}{16}-1=\frac{25}{144}-1=-\frac{119}{144}\)

Hệ số biến dạng theo mỗi trục đo O'x', O'y', O'z' lần lượt là:
p=O'A'OA=22=1�=�'�'��=22=1;
q=O'B'OB=13�=�'�'��=13;
r=O'C'OC=46=23�=�'�'��=46=23.

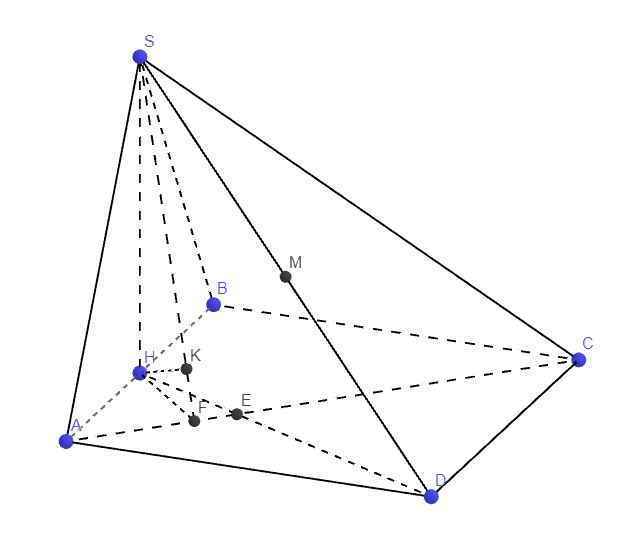
Gọi H là trung điểm AB, có lẽ từ 2 câu trên ta đã phải chứng minh được \(SH\perp\left(ABCD\right)\)
Do \(\left\{{}\begin{matrix}DM\cap\left(SAC\right)=S\\MS=\dfrac{1}{2}DS\end{matrix}\right.\) \(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)\)
Gọi E là giao điểm AC và DH
Talet: \(\dfrac{HE}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow HE=\dfrac{1}{2}DE\)
\(\left\{{}\begin{matrix}DH\cap\left(SAC\right)=E\\HE=\dfrac{1}{2}DE\end{matrix}\right.\) \(\Rightarrow D\left(H;\left(SAC\right)\right)=\dfrac{1}{2}d\left(D;\left(SAC\right)\right)=d\left(M;\left(SAC\right)\right)\)
Từ H kẻ HF vuông góc AC (F thuộc AC), từ H kẻ \(HK\perp SF\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H;\left(SAC\right)\right)\)
ABCD là hình vuông \(\Rightarrow\widehat{HAF}=45^0\Rightarrow HF=AH.sin45^0=\dfrac{a\sqrt{2}}{4}\)
\(SH=\dfrac{a\sqrt{3}}{2}\), hệ thức lượng:
\(HK=\dfrac{SH.HF}{\sqrt{SH^2+HF^2}}=\dfrac{a\sqrt{21}}{14}\)
\(\Rightarrow d\left(M;\left(SAC\right)\right)=\dfrac{a\sqrt{21}}{14}\)

a.
\(sin\left(2x-\dfrac{\pi}{4}\right)=-1\)
\(\Leftrightarrow2x-\dfrac{\pi}{4}=-\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{8}+k\pi\) (1)
\(-\dfrac{\pi}{3}\le x\le\dfrac{7\pi}{3}\Rightarrow-\dfrac{\pi}{3}\le-\dfrac{\pi}{8}+k\pi\le\dfrac{7\pi}{3}\)
\(\Rightarrow-\dfrac{5}{24}\le k\le\dfrac{59}{24}\Rightarrow k=\left\{0;1;2\right\}\)
Thế vào (1) \(\Rightarrow x=\left\{-\dfrac{\pi}{8};\dfrac{7\pi}{8};\dfrac{15\pi}{8}\right\}\)

ĐKXĐ: \(-2\le x\le3\)
Đặt \(\sqrt{x+2}+2\sqrt{3-x}=a\Rightarrow4\sqrt{6+x-x^2}-3x=a^2-14\)
Mặt khác \(a^2=\left(\sqrt{x+2}+2\sqrt{3-x}\right)^2\le5\left(x+2+3-x\right)=25\)
\(\Rightarrow a\le5\)
Và \(\sqrt{x+2}+\sqrt{3-x}+\sqrt{3-x}\ge\sqrt{5}+\sqrt{3-x}\ge\sqrt{5}\) \(\Rightarrow a\ge\sqrt{5}\)
\(\Rightarrow\sqrt{5}\le a\le5\)
Phương trình trở thành:
\(a^2-14=ma\Leftrightarrow\frac{a^2-14}{a}=m\) với \(a\in\left[\sqrt{5};5\right]\)
\(f\left(a\right)=\frac{a^2-14}{a}\Rightarrow f'\left(a\right)=\frac{2a^2-a^2+14}{a^2}=\frac{a^2+14}{a^2}>0\)
\(\Rightarrow f\left(a\right)\) đồng biến \(\Rightarrow f\left(\sqrt{5}\right)\le f\left(a\right)\le5\)
\(\Rightarrow-\frac{9\sqrt{5}}{5}\le f\left(a\right)\le\frac{11}{5}\Rightarrow-\frac{9\sqrt{5}}{5}\le m\le\frac{11}{5}\)










b: Chọn mp(SAC) có chứa SC
\(I\in SA\subset\left(SAC\right);I\in\left(BIK\right)\)
Do đó: \(I\in\left(SAC\right)\cap\left(BIK\right)\)
Trong mp(ABCD), gọi H là giao điểm của AC và BK
=>\(H\in\left(SAC\right)\cap\left(BIK\right)\)
=>\(\left(SAC\right)\cap\left(BIK\right)=HI\)
Gọi M là giao điểm của HI với SC
=>M là giao điểm của SC với mp(BIK)