Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

là đơn vị khoảng cách từ điểm x đến điểm 0 trên trục số
\(x\in Q:\left|x\right|\ge0;\left|x\right|=-x;\left|x\right|\ge x\)

Nếu \(a\) là số gần đúng của số đúng \(\overline{a}\) thì \(\Delta_a=\left|\overline{a}-a\right|\) được gọi là sai số tuyệt đối của số gần đúng \(a\).
Nếu \(\Delta_a=\left|\overline{a}-a\right|\le d\) thì \(-d\le\overline{a}-a\le d\) hay \(a-d\le\overline{a}\le a+d\) .
Ta nói \(a\) là số gần đúng của \(\overline{a}\) với độ chính xác \(d\), và quy ước viết gọn là \(\overline{a}=a\pm d\).

1/ Tinh ∆. Pt co 2 nghiem x1,x2 <=> ∆>=0.
Theo dinh ly Viet: S=x1+x2=-b/a=m+3.
Theo gt: |x1|=|x2| <=> ...
2/ \(\frac{\sin^2x-\cos^2x}{1+2\sin x.\cos x}\)
\(=\frac{\cos^2x\left(\frac{\sin^2x}{\cos^2x}-\frac{\cos^2x}{\cos^2x}\right)}{\cos^2x\left(\frac{1}{\cos^2x}+\frac{2\sin x.\cos x}{\cos^2x}\right)}\)
\(=\frac{\tan^2x-1}{\tan^2x+1+2\tan x}\)
\(=\frac{\left(\tan x-1\right)\left(\tan x+1\right)}{\left(\tan x+1\right)^2}\)
\(=\frac{\tan x-1}{\tan x+1}\left(dpcm\right)\)
c/ A M C B N BC=8 AC=7 AB=6
- Ta có: \(\overrightarrow{BA}^2=\left(\overrightarrow{CA}-\overrightarrow{CB}\right)^2\)
\(\Leftrightarrow BA^2=CA^2-2\overrightarrow{CA}.\overrightarrow{CB}+CB^2\)
\(\Leftrightarrow\overrightarrow{CA}.\overrightarrow{CB}=\frac{CA^2+CB^2-BA^2}{2}=\frac{77}{2}\)
- \(\overrightarrow{MN}^2=\left(\overrightarrow{CN}-\overrightarrow{CM}\right)^2=\left(\frac{3}{2}\overrightarrow{CB}-\frac{5}{7}\overrightarrow{CA}\right)^2\)
\(\Leftrightarrow MN^2=\frac{9}{4}CB^2-\frac{15}{7}\overrightarrow{CA}.\overrightarrow{CB}+\frac{25}{49}CA^2\)
\(=\frac{9}{4}.64-\frac{15}{7}.\frac{77}{2}+\frac{25}{49}.49\)
\(=\frac{173}{2}\)
\(\Rightarrow MN=\sqrt{\frac{173}{2}}=\frac{\sqrt{346}}{2}\)

Giá trị tuyệt đối của một số là khoảng cách của số đó đến điểm 0 trên trục số nằm ngang.
|0| = 0; |1,25| = 1,25;
|(-3)/4| = 3/4; |-π| = π

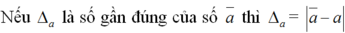
được gọi là sai số tuyệt đối của số gần đúng a.
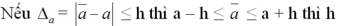
được gọi là độ chính xác của số gần đúng a.
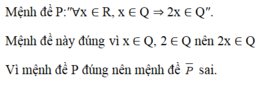
giá trị tuyệt đối của số hữu tỉ X, được xác định : số đơn vị từ điểm 0 đến x