Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: x2>=0(với mọi x)
=>2x-x2<=2x(với mọi x)
->(2x-x2)(x+2)(x+4)<=(2x)(x+2)(x+4)(với mọi x) hay A<=(2x)(x+2)(x+4)
Do đó, GTLN của A khi x =0 là (2x)(x+2)(x+4) hay 0(x+2)(x+4) hay 0
Vậy GTLN của A là 0 khi x=0
\(\left(2x-5\right)^2<\left(2x-1\right)\left(2x+1\right)-\frac{5}{4}\Leftrightarrow4x^2-20x+25<4x^2-1-\frac{5}{4}\)
<=>-20x+25<-9/4
<=>-20x<-109/4
<=>x>109/80=1,3625
Vậy giá trị x cần tìm là: 2
\(P=\left(4a^2+b^2+4ab-12a-6b+9\right)+\left(3b^2-6b+3\right)\)
\(P=\left(2a+b-3\right)^2+3\left(b-1\right)^2\ge0\)
Đẳng thức xẩy ra khi: \(\left\{\begin{matrix}\left(b-1\right)=0\\2a+b-3=0\end{matrix}\right.\Leftrightarrow\left\{\begin{matrix}b=1\\a=1\end{matrix}\right.\)
Kết luận: GTNN P=0 khi a=b=1
[(4a^2 - 12a + 9) + 2b(2a - 3) + b^2] + 3b^2 - 6b + 3
= (2a - 3 + b)^2 + 3(b-1)^2
=> P nhỏ nhất = 0 khi (2a - 3 + b) = 3(b-1) = 0
tick cho mk nha
P= \(\frac{2n+1}{n+1}\)= \(\frac{2n+2-1}{n+1}\) = \(\frac{2n+2}{n+1}\) - \(\frac{1}{n-1}\) = 2- \(\frac{1}{n-1}\)
a) Vì 2 thuộc Z nên để P thuộc Z thì \(\frac{1}{n-1}\) phải thuộc Z
=> 1 chia hết cho n-1 => n-1 thuộc Ư(1)={1;-1}
TH1:n-1=1 => n=2
TH2:n-1=-1 => n=0. Vậy n thuộc {2;0}
- b) Vì 2 thuộc Z nên để P có GTLN thì -\(\frac{1}{n-1}\) có GTLN => \(\frac{1}{n-1}\) có GTNN
Ta có: 1 thuộc Z và \(\frac{1}{n-1}\) có GTNN => n-1 là số nguyên âm lớn nhất => n-1=-1 => n=0
Khi đó, P= \(\frac{2.0+1}{0+1}\) = \(\frac{1}{1}\)= 1
- Vì 2 thuộc Z nên để P có GTNN thì - \(\frac{1}{n-1}\) có GTNN => \(\frac{1}{n-1}\) có GTLN
=> n-1 là số nguyên dương nhỏ nhất => n-1=1 => n=2
Khi đó, P= \(\frac{2.2+1}{2+1}\)= \(\frac{5}{3}\)
P thuộc Z khi: 2n+1 chia hết cho n+1
<=> 2n+2-1 chia hết cho n+1<=> 2(n+1)-1 chia hết cho n+1
<=> 1 chia hết cho n+1 (vì: 2(n+1) chia hết cho n+1)
<=> n+1 E {-1;1} <=> n E {-2;0}. Vậy: n E {-2;0} P/S: E là thuộc nha!
b)\(P=\frac{2n+1}{n+1}=\frac{2n+2-1}{n+1}=2-\frac{1}{n+1}\)
+)P lớn nhất khi n+1 là số nguyên âm lớn nhất => n+1=-1=>n=-2
Thay vào ta được:
\(P_{max}=2-\frac{1}{-1}=2-\left(-1\right)=3\)
+)P nhỏ nhất khi n+1 là số nguyên dương bé nhất=>n+1=1=>n=0
Thay vào ta được:
\(P_{min}=2-\frac{1}{1}=2-1=1\)
\(P=4a^2+4ab+4b^2-12a-12b+12=\left[\left(4a^2-12a+9\right)+2b\left(2a-3\right)+b^2\right]+3b^2-6b+12\\ =\left(2a+b-3\right)^2+3\left(b-1\right)^2+9\)
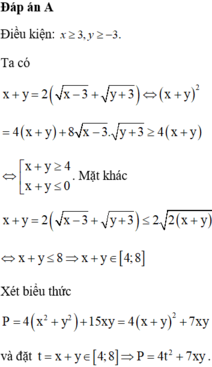
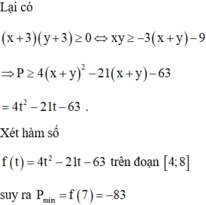
\(A=\left(2x-4\right)^2-4\left|4-2x\right|+1986=\left(2x-4\right)^2-4\left|2x-4\right|+1986\)
Ta thấy: \(\left|2x-4\right|^2=\left(2x-4\right)^2\)
Đặt t=|2x-4| ta được: t2=(2x-4)2
Suy ra: A=t2-4t+1986=t2-4t+4+1982
=(t-2)2+1982 \(\ge\)1982 (với mọi x)
Dấu "=" xảy ra khi: t=2
<=>|2x-4|=2
Với x\(\ge\)0 ta được: 2x-4=2 <=> x=3
Với x<0 ta được: 4-2x=-2 <=> x=3 (loại)
Vậy GTNN của A là 1982 tại x=3
3 nhe