
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3) tổng có số ước la (10 +1)(1 + 1) = 11.2 = 22 ước dó
2) ta có x( x - 3) < 0 nên x và x -3 trái dấu nhau mặt khác x > x-3 nên :
x > 0 và x - 3 < 0 => x < 3 vạy chung lại ta có 0 < x < 3 do x nguyên nên x = 1, x = 2

\(2x+4⋮x-1\Rightarrow2\left(x-1\right)+6⋮x-1\)
\(\Rightarrow6⋮x-1\Rightarrow x-1\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
\(\Rightarrow x\in\left\{2;0;3;-1;4;-2;7;-5\right\}\)
Vậy...........................................
\(2x^2+\left(-3\right)^2=41\)
\(\Rightarrow2x^2=41-9=32\)
\(\Rightarrow x^2=16\)
\(\Rightarrow x=\pm4\)
\(2\left(x-5\right)-3\left(x+7\right)=14\)
\(\Rightarrow2x-10-3x-21=14\)
\(\Rightarrow2x-3x=14+21+10\)
\(\Rightarrow-x=45\Rightarrow x=-45\)
\(-7\left(5-x\right)-2\left(x-10\right)=15\)
\(\Rightarrow-35+x-2x+20=15\)
\(\Rightarrow x-2x=15-20+35\)
\(\Rightarrow-x=30\Rightarrow x=-30\)

a) \(x\in\left\{-1;0;1;2;3;4;\right\}\)
b) \(x\in\left\{-6;-5;-4;-3;-2;-1\right\}\)
c) \(x\in\left\{1;2;3;4;5;6;7\right\}\)
d) \(x\in\left\{-1;0;1;2;3;4;5\right\}\)

a) ( x + 3 )3 : 3 - 1 = -10
( x + 3 )3 : 3 = -10 + 1
( x + 3 )3 = -9 * 3
x + 3 = \(\sqrt[3]{-27}\)
x = -3 - 3
x = -6
b) 3 | x - 1 | + 5 = 17
3 | x - 1 | = 17 - 5
| x - 1 | = 12 : 3
| x - 1 | = 4
( 1 ) x - 1 > 0 => x - 1 = 4 => x = 5
( 2 ) x - 1 < 0 => x - 1 = -4 => x = -3
Vậy S = { -3 ; 5 }

Lí luận chung cho cả 4 câu :
Để tích này bé hơn 0 thì các thừa số phải trái dấu với nhau
a) Dễ thấy \(x-2>x-7\)
\(\Rightarrow\hept{\begin{cases}x-2>0\\x-7< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>2\\x< 7\end{cases}\Leftrightarrow}2< x< 7}\)
b) tương tự
c) \(\left(x^2-1\right)\left(x^2-4\right)\left(x^2-7\right)\left(x^2-10\right)< 0\)
\(\Leftrightarrow\left(x^4-11x^2+10\right)\left(x^4-11x^2+28\right)< 0\)
Dễ thấy \(x^4-11x^2+10< x^4-11x^2+28\)
\(\Rightarrow\hept{\begin{cases}x^4-11x^2+10< 0\\x^4+11x^2+10>0\end{cases}}\)
Tự giải nốt nha bạn mình bận rồi


a) \(\left(x^2-5\right)\left(x^2-25\right)< 0\)
Vì \(x^2-5>x^2-25\) nên \(\left\{{}\begin{matrix}x^2-5>0\\x^2-25< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2>5\\x^2< 25\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\sqrt{5}< x< -\sqrt{5}\left(vl\right)\\-5< x< 5\end{matrix}\right.\)
b) \(\left(x+5\right)\left(9+x^2\right)< 0\)
Vì \(9+x^2>0\) nên \(x+5< 0\Leftrightarrow x< -5\)
c) \(\left(x+3\right)\left(x^2+1\right)=0\)
Vì \(x^2+1>0\) nên \(x+3=0\Leftrightarrow x=-3\)
d) \(\left(x+5\right)\left(x^2-4\right)=0\)
\(\Rightarrow\left(x+5\right)\left(x+2\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-5\\x=-2\\x=2\end{matrix}\right.\)
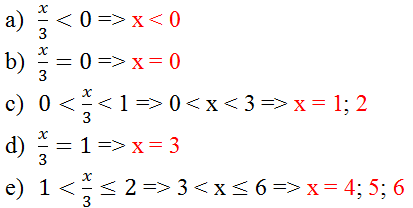
Chọn D