HT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HT
1
28 tháng 9 2016
Ta có :
\(x^2-46x+45\)
\(=\left(x^2-45x\right)-\left(x-45\right)=0\)
\(\left(x-1\right)\left(x-45\right)=0\)
\(\orbr{\begin{cases}x=1\\x=45\end{cases}}\)
Mà x lớn nhất nên x =45
Vậy ...
CM
27 tháng 6 2019
7 x 2 (x – 7) + 5x(7 – x) = 0
ó 7x.x(x – 7) – 5.x(x – 7) = 0
ó (7x.x – 5.x)(x – 7) = 0
ó x(7x – 5)(x – 7) = 0
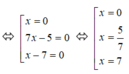
Giá trị lớn nhất của x thỏa mãn đề bài là x = 7.
Đáp án cần chọn là: B
TN
3 tháng 11 2016
Câu 1:(3x+2)(4x-5)=0
\(\Leftrightarrow\orbr{\begin{cases}3x+2=0\\4x-5=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{2}{3}\\x=\frac{5}{4}\end{cases}}\)
Câu 2:
x3+5x2+3x-9=0
<=>x3+6x2+9x-x2-6x-9=0
<=>x(x2+6x+9)-(x2+6x+9)=0
<=>(x-1)(x2+6x+9)=0
<=>(x-1)(x+3)2=0
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\\left(x+3\right)^2=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)
TN
3 tháng 11 2016
Câu 2: bổ sung thêm phần cuối
Tổng các giá trị x thỏa mãn là (-3)+1=-2
CM
13 tháng 9 2018
Ta có
25 x 4 – x 2 = 0 ⇔ 25 x 2 . x 2 – x 2 + . 1 = 0 ⇔ x 2 ( 25 x 2 – 1 ) = 0
ó x 2 = 0 25 x 2 - 1 = 0
ó x 2 = 0 x 2 = 1 25 ó x = 0 x = 1 5 x = - 1 5 suy ra x 0 = 1 5 => x 0 < 1
Đáp án cần chọn là: A
3 tháng 5 2019
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
4 tháng 5 2019
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
KT
1
4 tháng 2 2022
\(x^2=2^4\)
nên \(x^2=16\)
=>x=4(loại) hoặc x=-4(nhận)
\(x^2-46x+45=0\)
\(\Leftrightarrow\left(x^2-45x\right)-\left(x-45\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-45\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x-1=0\\x-45=0\end{array}\right.\Leftrightarrow\left[\begin{array}{nghiempt}x=1\\x=45\end{array}\right.\)
Mà x là GTLN nên \(x=45\)
x2-46x+45=0
Hoặc x2-2.23.x+232-484=0
(x-23)2=484
x-23=22
x=45
Vậy x=45