Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
PT hoành độ giao điểm: $mx^2=x-2$
$\Leftrightarrow mx^2-x+2=0(*)$
Để 2 đths cắt nhau tại 2 điểm phân biệt thì pt $(*)$ phải có 2 nghiệm phân biệt
Điều này xảy ra khi \(\left\{\begin{matrix} m\neq 0\\ \Delta=1-8m>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m\neq 0\\ m< \frac{1}{8}\end{matrix}\right.(I)\)
Hoành độ giao điểm khi đó là 2 nghiệm $x_1,x_2$ của pt $(*)$
Áp dụng định lý Viet: $x_1+x_2=\frac{1}{m}; x_1x_2=\frac{2}{m}$
Để 2 điểm phân biệt nằm ở 2 phía của trục tung thì $x_1,x_2$ trái dấu
Tức là $x_1x_2<0\Leftrightarrow\frac{2}{m}<0$
$\Leftrightarrow m<0$
Kết hợp với $(I)$ suy ra $m<0$
\(Bước 1\) Lập phương trình hoành độ
Hoành độ giao điểm là nghiệm của pt
\(x-2=mx^2\\ \Leftrightarrow-mx^2+x-2=0\)
\(Bước2\) Để hai hàm số cắt nhau tại hai điểm phân biệt nằm về hai phía của trục tung => pt có 2 nghiệm trái dấu
\(a\times c< 0\\ \Leftrightarrow\left(-m\right).\left(-2\right)< 0\\ \Leftrightarrow2m< 0\\ \Leftrightarrow m< 0\\ =>B\)

Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=3m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=10\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=10\)
\(\Leftrightarrow4-2\left(3m-1\right)=10\)
\(\Leftrightarrow m=-\dfrac{2}{3}\)

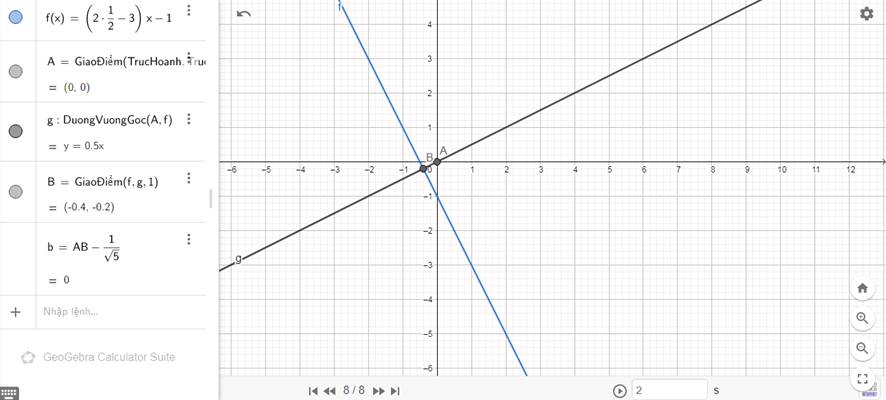
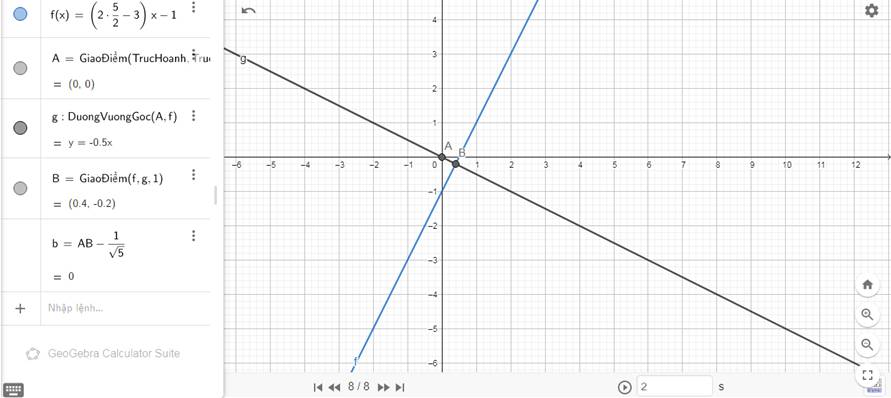
- Gọi M(x0,y0) ,N(x1,y1) lần lượt là giao điểm của đường thẳng (d): \(y=\left(2m-3\right)x-1\) với trục tung, trục hoành \(\Rightarrow x_0=y_1=0\).
Vì M(0;y0) thuộc (d) nên: \(y_0=\left(2m-3\right).0-1=-1\)
\(\Rightarrow M\left(0;-1\right)\) nên \(OM=1\) (đvđd)
\(N\left(x_1;0\right)\) thuộc (d) nên: \(\left(2m-3\right)x_1-1=0\Rightarrow x_1=\dfrac{1}{2m-3}\)
\(\Rightarrow N\left(\dfrac{1}{2m-3};0\right)\) nên \(ON=\dfrac{1}{2m-3}\) (đvđd)
*Hạ OH vuông góc với (d) tại H \(\Rightarrow OH=\dfrac{1}{\sqrt{5}}\)
Xét △OMN vuông tại O có OH là đường cao.
\(\Rightarrow\dfrac{1}{OM^2}+\dfrac{1}{ON^2}=\dfrac{1}{OH^2}\)
\(\Rightarrow1+\left(2m-3\right)^2=5\)
\(\Rightarrow2m-3=\pm2\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=\dfrac{1}{2}\end{matrix}\right.\) (nhận)

Vì đồ thị hàm số y=ax+b song song với đường thẳng \(y=\dfrac{2}{3}x+1\) nên \(\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b\ne1\end{matrix}\right.\)
hay hàm số có dạng là \(y=\dfrac{2}{3}x+b\)
Vì đồ thị hàm số \(y=\dfrac{2}{3}x+b\) cắt trục tung tại điểm có tung độ bằng -1 nên
Thay x=0 và y=-1 vào hàm số \(y=\dfrac{2}{3}x+b\), ta được:
\(\dfrac{2}{3}\cdot0+b=-1\)
\(\Leftrightarrow b=-1\)
Vậy: Hàm số có dạng là \(y=\dfrac{2}{3}x-1\)
- Thấy đường thẳng song song với \(y=\dfrac{2}{3}x+1\)
\(\Rightarrow\left\{{}\begin{matrix}a=a^,\\b\ne b^,\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\b\ne1\end{matrix}\right.\)
=> Phương trình đường thẳng có dạng : \(y=\dfrac{2}{3}x+b\)
Lại có đồ thị cắt trục tung tại điểm có tung độ là - 1
=> b = -1 ( TM )
Vậy phương trình đường thẳng cần tìm có dạng : \(y=\dfrac{2}{3}x-1\)

Gọi (d'): y = ax + b
Do (d') // (d) nên a = -1/2
⇒ (d'): y = -x/2 + b
Do (d') cắt trục hoành tại điểm có hoành độ là 3 nên thay x = 3; y = 0 vào (d') ta có:
-3/2 + b = 0
⇔ b = 3/2
Vậy (d'): y = -x/2 + 3/2

2 đồ thị song song \(\Leftrightarrow\left\{{}\begin{matrix}m-\dfrac{2}{3}=2-m\\3\ne n-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{4}{3}\\n\ne4\end{matrix}\right.\)

a: Thay x=2 và y=-3 vào (d), ta được:
\(2\left(2m-1\right)-2m+5=-3\)
=>\(4m-2-2m+5=-3\)
=>2m+3=-3
=>2m=-6
=>\(m=-\dfrac{6}{2}=-3\)
b: Để (d)//(d') thì \(\left\{{}\begin{matrix}2m-1=2\\-2m+5\ne1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2m=3\\-2m\ne-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=\dfrac{3}{2}\\m\ne2\end{matrix}\right.\)
=>m=3/2
Thay m=3/2 vào (d), ta được:
\(y=\left(2\cdot\dfrac{3}{2}-1\right)x-2\cdot\dfrac{3}{2}+5=2x+2\)

y=2x+2 nên a=2
Gọi \(\alpha\) là góc tạo bởi (d) với trục Ox
\(tan\alpha=2\)
=>\(\alpha\simeq63^026'\)

Vì (d)//y=-3x+2 nên a=-3
Vậy: (d): y=-3x+b
Thay \(x=-\dfrac{1}{3}\) và y=0 vào (d), ta được:
\(b-3\cdot\dfrac{-1}{3}=0\)
hay b=-1

a: a=-2 nên y=-2x+b
Thay x=2,5 và y=0 vào y=-2x+b, ta được:
\(b-2\cdot2,5=0\)
=>b-5=0
=>b=5
Vậy: y=-2x+5
b: a=3 nên y=3x+b
Thay x=0 và y=-4/3 vào y=3x+b, ta được:
\(b+3\cdot0=-\dfrac{4}{3}\)
=>\(b=-\dfrac{4}{3}\)
Vậy: \(y=3x-\dfrac{4}{3}\)
c: Vì đồ thị hàm số y=ax+b song song với đường thẳng y=-4x+3 nên \(\left\{{}\begin{matrix}a=-4\\b\ne3\end{matrix}\right.\)
Vậy: y=-4x+b
Thay x=-1 và y=8 vào y=-4x+b, ta được:
\(b-4\cdot\left(-1\right)=8\)
=>b+4=8
=>b=4
vậy: y=-4x+4
d: Thay x=0 và y=4 vào y=ax+b, ta được:
\(a\cdot0+b=4\)
=>b=4
Vậy: y=ax+4
Thay x=2 và y=3 vào y=ax+4, ta được:
\(a\cdot2+4=3\)
=>2a=3-4=-1
=>\(a=-\dfrac{1}{2}\)
Vậy: \(y=-\dfrac{1}{2}x+4\)
e: Thay x=0 và y=-2 vào y=ax+b, ta được:
\(a\cdot0+b=-2\)
=>b=-2
=>y=ax-2
Thay x=1 vào y=-4x+3, ta được:
\(y=-4\cdot1+3=-4+3=-1\)
Thay x=1 và y=-1 vào y=ax-2, ta được:
\(a\cdot1-2=-1\)
=>a-2=-1
=>a=1
Vậy: y=x-2
Để đò thị hàm số `y=(2m-3)x+2` song song với trục hoành thì:
`2m-3=0`
`<=>m= 3/2`
`=>C`