Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1>\(\Delta=b^2-4ac\)
\(=m^2-4\left(2m-1\right)\left(-m+1\right)\)
khai triển ra là được \(\left(3m-2\right)^2\ge0\)
=>phương trình luôn có ít nhất là một nghiệm
2>để phương trình có 2 nghiệm phân biệt thì \(\left(3m-2\right)^2>0\)=>\(3m-2>0\Rightarrow m>\frac{2}{3}\)
còn cần tìm x thì theo công thức mà tìm
3> thế vô mà tìm

a. 5x2 + 2mx – 2m +15 =0 (1)
Ta có: Δ'=m2 – 5.(-2m +15) = m2 +10m -75
Phương trình (1) có nghiệm kép khi và chỉ khi:
Δ'= 0 ⇔ m2 + 10m – 75 = 0
Δ'm = 52 -1.(-75) = 25 +75 = 100 > 0
√(Δ'm) = √100 =10
Phương trình có 2 nghiệm phân biệt:
Vậy m =5 hoặc m=-15 thì phương trình đã cho có nghiệm kép
b. mx2 – 4(m -1)x -8 =0 (2)
Phương trình (2) có nghiệm kép khi và chỉ khi: m≠ 0 và Δ'=0
Ta có: Δ'=[-2(m-1)]2 – m(-8)=4(m2 -2m +1) +8m
=4m2– 8m +4 +8m = 4m2 +4
Vì 4m2 +4 luôn luôn lớn hơn 0 nên Δ' không thể bằng 0 .Vậy không có giá trị nào của m để phương trình có nghiệm kép

\(\Delta'=b'^2-ac=-6m+7=>\)\(m\ge\frac{7}{6}\)
Theo Vi-ét : \(\hept{\begin{cases}x_1+x_2=2\left(m-2\right)\\x_1.x_2=m^2+2m-3\end{cases}}\)Mà \(\frac{1}{x_1}+\frac{1}{x_2}=\frac{x_1+x_2}{5}=>\)\(\frac{x_1+x_2}{x_1.x_2}=\frac{x_1+x_2}{5}\)
=> \(x_1.x_2=5\)<=> \(m^2+2m-3=5\)<=> \(m^2+2m-8=0\)
Giải pt trên ta đc : \(\orbr{\begin{cases}m=2\\m=-4\end{cases}}\)Mà \(m\ge\frac{7}{6}\)=> \(m=2\)


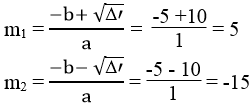
\(x^2\left(x-5\right)>4-5x\)
\(\Leftrightarrow x^3-5x^2+5x-4>0\)
\(\Leftrightarrow\left(x-4\right)\left(x^2-x+1\right)>0\)
\(\Leftrightarrow x-4>0\) (do \(x^2-x+1=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}>0;\forall x\))
\(\Rightarrow x>4\)
Để 2 BPT có cùng tập nghiệm thì \(mx-5>x-2m\) có nghiệm \(x>4\)
\(mx-x>-2m+5\)
\(\Leftrightarrow\left(m-1\right)x>-2m+5\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>1\\x>\frac{-2m+5}{m-1}\\\frac{-2m+5}{m-1}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>1\\-2m+5=4m-4\end{matrix}\right.\) \(\Rightarrow m=\frac{3}{2}\)
Test