Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

góc ADB=180-73-48=59 độ
AB/sin59=DA/sin48=DB/sin73
=>DA=26,0(m); DB=33,47(m)
S ABC=1/2*26*33,47*sin59=372,96m2
=>AH=2*372,96:30=24,864(m)

Gọi chiều cao tháp và bóng lúc tia sáng hợp với mặt đất góc 24 độ là x, y thì ta có hệ
\(\hept{\begin{cases}x=y.tan24^o\\x=\left(y+8,5\right).tan20^o\end{cases}}\)

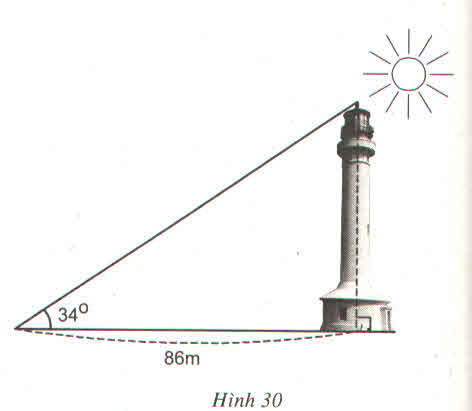
Gọi a là chiều cao của tháp, ta có:
\(\tan34\) = \(\dfrac{c.đối}{c.kề}\)= \(\dfrac{a}{86}\)
\(\Rightarrow a=\) \(\tan34.86\) \(\approx\) 58m
Vậy chiều cao của tháp là 58m

Gọi chiều cao của tháp là AB, bóng của tòa tháp trên mặt đất là AC.
Theo đề, ta có: AB\(\perp\)AC tại A, \(\widehat{C}=45^0\); AC=30m
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}\)
=>\(\dfrac{AB}{30}=tan45=1\)
=>AB=30(m)
=>Chọn A

A B C D I H 30 0
a) Ta thấy điểm C nằm trên nửa đường tròn đường kính AB => ^ACB = 900
Hay ^ACI = 900 . Xét \(\Delta\)AIC có: ^ACI = 900 ; ^CAI (=^CAD) = 300
=> IA= 2.IC => \(\frac{IC}{IA}=\frac{1}{2}\)
Xét \(\Delta\)CID và \(\Delta\)AIB có: ^CID = ^AIB (Đối đỉnh); ^ICD = ^IAB (2 góc nội tiếp chắn cung BD)
=> \(\Delta\)CID ~ \(\Delta\)AIB (g.g) => \(\frac{CD}{AB}=\frac{IC}{IA}=\frac{1}{2}\).
Vậy \(\frac{CD}{AB}=\frac{1}{2}.\)
b) Xét tứ giác ACIH: ^ACI = 900; ^AHI = 900 => Tứ giác ACIH nội tiếp đường tròn
=> ^IAH = ^ICH hay ^BAD = ^ICH. Mà ^BAD = ^BCD (2 góc nội tiếp chắn cung BD)
=> ^ICH = ^BCD = ^ICD => CI là phân giác ^DCH.
Chứng minh tương tự; ta có: DI là phân giác ^CDH
Xét \(\Delta\)CDH có: CI là phân giác ^DCH; DI là phân giác ^CDH
=> I là giao điểm của 3 đường phân giác của \(\Delta\)CDH (đpcm).

\(cot48^0=cot\widehat{CBD}=\frac{BC}{CD}=\frac{AC+30}{CD}=0,9\)
\(cot73^0=\frac{AC}{CD}=0,31\)
\(\Rightarrow\frac{AC}{CD}+\frac{30}{CD}=0,9\Rightarrow\frac{30}{CD}=0,9-0,31\approx0,6\)
\(\Rightarrow CD=\frac{30}{0,6}\approx50\left(m\right)\)