Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\frac{3^7.5^4.7^9}{3^3.5^2.7^5}\)
\(=3^4.5^2.7^4\)
= ... ( tính máy )
\(\frac{\left(3^2.5.7^9\right)\left(5^3.3^5\right)}{3^3.5^2.7^5}\)
\(=\frac{\left(3^7.5^4.7^9\right)}{3^3.5^2.7^5}\)
\(=3^4.5^2.7^4\)
\(=81.25.2401\)
\(=\text{4862025}\)

\(\frac{2^3.5.7.5^2.7^3}{2^2.5^2.7^4}=\frac{2^3.5^3.7^4}{2^2.5^2.7^4}=2.5=10\)
đối với lớp 6 thì trình bày thế này dễ hiểu hơn
\(\frac{\left(2^3.5.7\right)\left(5^2.7^3\right)}{\left(2.5.7^2\right)^2}=\frac{2^3.5.5^2.7.7^3}{2.5.7^2.2.5.7^2}=\frac{2^3.5^3.7^4}{2^2.5^2.7^4}=\frac{2.5}{1}=10\)

=1,7.2,3+1,7.(-3,7)-1,7.3-1,7
=1,7.[2,3+(-3,7)-3-1]
=1,7.(-5,4)
= -9,18
a, \(\frac{\left(2^3\cdot5\cdot7\right)\cdot\left(5^2\cdot7^3\right)}{\left(2\cdot5\cdot7^2\right)^2}=\frac{2\cdot2^2\cdot5^2.5.7.7^2}{2\cdot5\cdot7^2}=\frac{1\cdot2^2\cdot5^2\cdot7^2}{1\cdot1\cdot1}=4900\)
b, \(1,7\cdot2,3+1,7\cdot\left(-3,7\right)-1,7.3-1,7:0,1=1,7\cdot\left(-3,7+2,3-3\right)-1,7:0,1=1,7.\left(-4,4\right)-1,7:0,1=\left(-2,7\right)-17=-19,7\)

câu trả lời của mình là 10!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

\(\frac{\left(2^3\cdot5\cdot7\right)\cdot\left(5^2\cdot7^3\right)}{\left(2\cdot5\cdot7^2\right)^2}\)
\(=\frac{2^3\left(5\cdot5^2\right)\left(7\cdot7^3\right)}{2^2\cdot5^2\cdot7^4}\)
\(=\frac{2^2\cdot2\cdot5\cdot5^2\cdot7^4}{2^2\cdot5^2\cdot7^4}\)
Triệt tiêu ta còn \(2\cdot5=10\)
\(\frac{\left(2^3.5.7\right).\left(5^2.7^2\right)}{\left(2.5.7^2\right)^2}\)
\(=\frac{2^3.\left(5.7\right).\left(5^2.7^3\right)}{2^2.5^2.7^4}\)
\(=\frac{2^2.2.5.5^2.7.7^3}{2^2.5^2.7^4}\)
\(=\frac{2^2.2.5.5^2.7^4}{2^2.5^2.7^4}\)
\(=2.5\)
\(=10\)

a/\(\frac{\left(2^3.5.7\right).\left(5^2.7^3\right)}{\left(2.5.7^2\right)^2}\)
=\(\frac{2^3.5^3.7^4}{2^2.5^2.7^4}\)
=2.5
=10
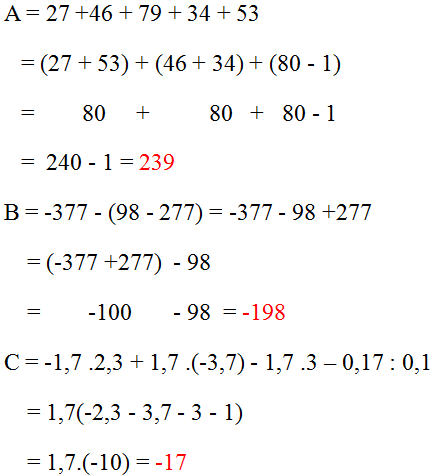
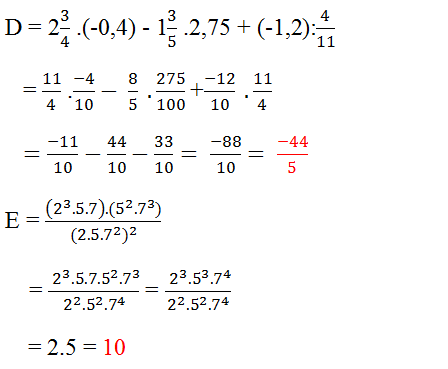
= \(\frac{3^2.5^4.7^9}{3^3.5^2.7^5.3^3.5^2.7^5}\)
=\(\frac{3^2.5^4.7^9}{3^6.5^4.7^{10}}\)
= \(\frac{1.1.1}{3^4.1.7}\)
= \(\frac{1}{567}\)
\(\frac{\left(3^2.5.7^9\right).\left(3^5.5^3\right)}{\left(3^3.5^2.7^5\right)^2}=\frac{\left(3^2.3^5\right).\left(5.5^3\right).7^9}{3^6.5^4.7^{10}}=\frac{3^7.5^4.7^9}{3^6.5^4.7^{10}}=\frac{3}{7}\)