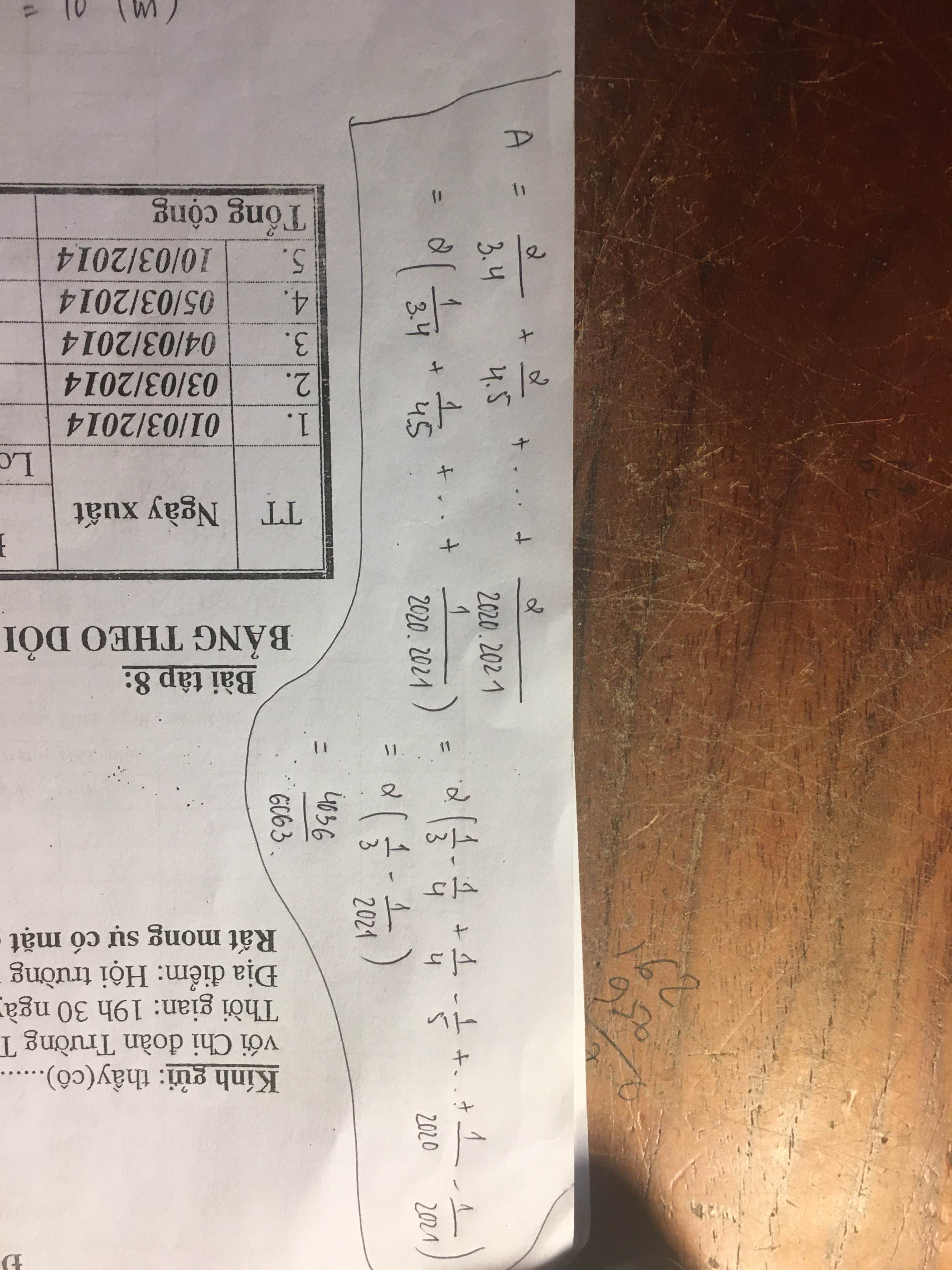
\(\frac{2}{3.4}+\frac{2}{4.5}+...+\frac{2}{2020.2021}\)các bạn làm cả cách giải nha mik cần cách làm cơmik sẽ tick cho 3...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Nguyễn Ngọc Tuấn Nam

VIP

5 tháng 4 2022 - olm

\(\frac{2}{3.4}+\frac{2}{4.5}+...+\frac{2}{2020.2021}\)

các bạn làm cả cách giải nha mik cần cách làm cơ

mik sẽ tick cho 3 ng nhanh nhứt

#Toán lớp 5

Nguyễn Thanh Hằng

5 tháng 4 2022

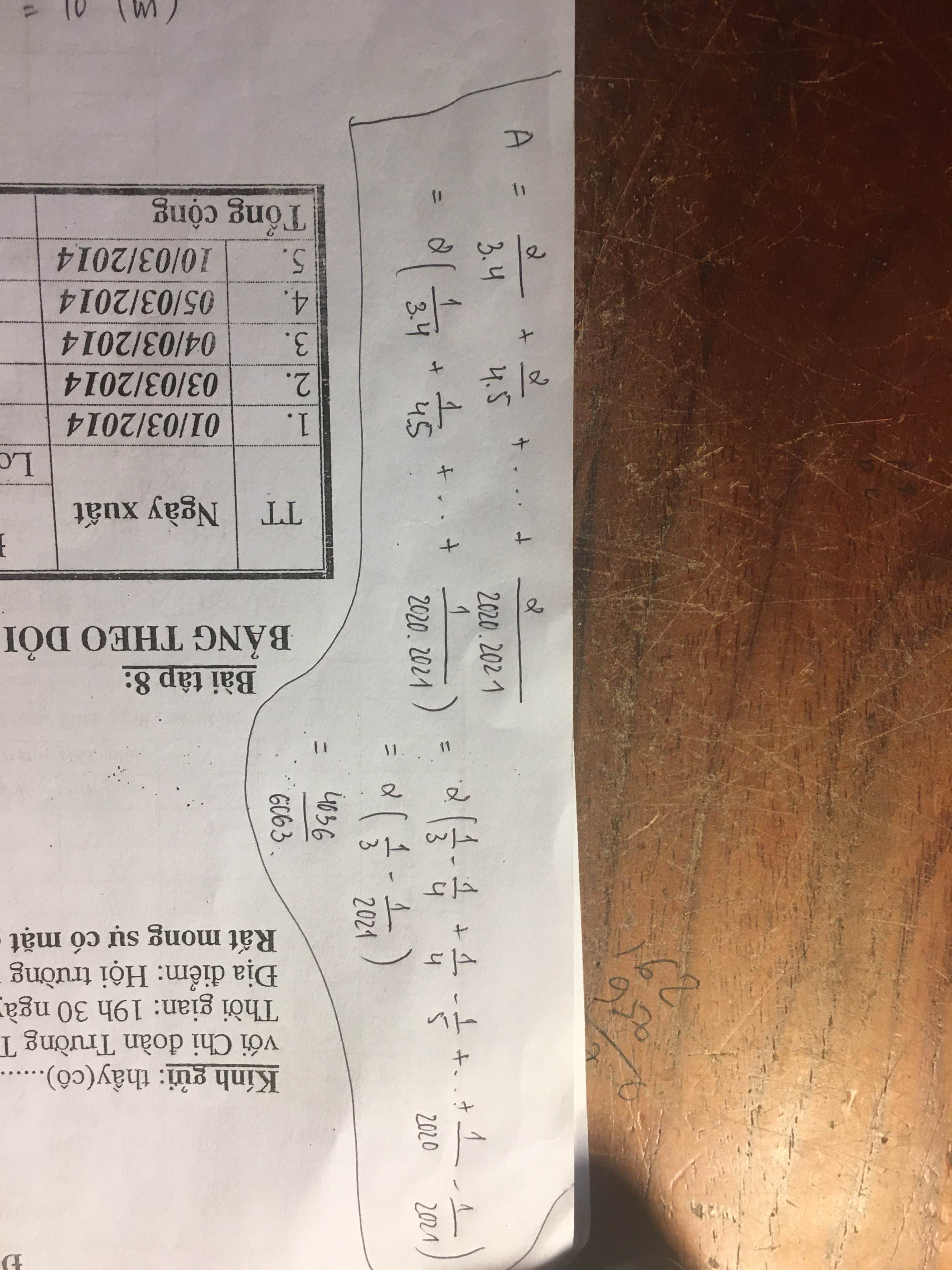
undefined

Đúng(1)

✎﹏l๏gคภlєє︵²ᵏ¹⁰

5 tháng 4 2022

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Nguyễn Đình Thoại

22 tháng 4 2017 - olm

Tính bằng cách thuận tiện nhất:

\(1\frac{4}{5}+2\frac{5}{7}+3\frac{4}{5}+4\frac{5}{7}\)

Các bạn làm nhanh và đúng cho mình với, mình đang gấp lắm!

Ai nhanh mình sẽ tick cho!

#Toán lớp 5

DanAlex

22 tháng 4 2017

Ta có: \(1\frac{4}{5}+2\frac{5}{7}+3\frac{4}{5}+4\frac{5}{7}\)

\(=\left(1\frac{4}{5}+3\frac{4}{5}\right)+\left(2\frac{5}{7}+4\frac{5}{7}\right)\)

\(=\left(\frac{9}{5}+\frac{19}{5}\right)+\left(\frac{19}{7}+\frac{33}{7}\right)\)

\(=\frac{28}{5}+\frac{52}{7}=13\frac{1}{35}\)

Đúng(0)

Nhok Lạnh Lùng

22 tháng 4 2017

= ( \(1\frac{4}{5}\)+ \(3\frac{4}{5}\)) + ( \(2\frac{5}{7}\)+ \(4\frac{5}{7}\))

= \(4\frac{4}{5}\) + \(6\frac{5}{7}\)

= \(\frac{24}{5}\) + \(\frac{47}{7}\)

= ...... ( tính nốt nhé )

Đúng(0)

Nguyễn Phương Thảo

18 tháng 9 2015 - olm

( 1999 * 1998 + 1998 * 1997) * ( 1 +\(\frac{1}{2}:\frac{3}{2}-\frac{4}{3}\)) = ?

Mình cần gấp lắm nên mong các bạn giải cả cách làm hộ mình nhé!

Thank you so much!

#Toán lớp 5

winx bloom

18 tháng 9 2015

mik học lớp 5 mik bít đấy

Đúng(0)

Linh Trịnh Khánh

30 tháng 3 2019 - olm

Bài 1: Tính Tổng B sau, biết

B = \(\frac{2}{3}+\frac{2}{15}+\frac{2}{35}+\frac{2}{63}+\frac{2}{99}+.......+\frac{2}{88803}+\frac{2}{89999}\)

Các Bạn Làm Nhanh Hộ Mình Nhé Ngày Mai Mình Phải Nộp Bài Rồi Bạn Nào Làm Nhanh Nhất Mình Tick Cho Nha

#Toán lớp 5

DoThah Trong

30 tháng 3 2019

B=2/1.3 + 2/3.5 + 2/5.7 +...+ 2/299.301

B=1-1/3+1/3-1/5+1/5-1/7+...+1/299-1/301=1-1/301=300/301

Đúng(0)

Hoàng Nguyễn

30 tháng 3 2019

\(Ta có: \frac{2}{3}=\frac{1}{1}-\frac{1}{3}\);

\(\frac{2}{15}=\frac{1}{3}-\frac{1}{5}\);

\(\frac{2}{35}=\frac{1}{5}-\frac{1}{7}\) ; ... ; \(\frac{2}{89999}=\frac{1}{299}-\frac{1}{301}\).

=> B= \(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{299}-\frac{1}{301}\)

=> B=\(\frac{1}{1}-\frac{1}{301}\)

=> B=\(\frac{300}{301}\)

Đúng(0)

nguyen phuong linh

3 tháng 4 2017 - olm

Tính bằng cách hợp lí:

\(\frac{1}{2009}+\frac{2}{2009}+\frac{3}{2009}+............+\frac{2008}{2009}\)

làm cả cách làm ra mình tick cho

#Toán lớp 5

Number one princess in the world

3 tháng 4 2017

Ta có :

\(\frac{1}{2009}+\frac{2}{2009}+....+\frac{2008}{2009}\)

\(=\frac{1+2+....+2008}{2009}\)

\(=\frac{2017036}{2009}=1004\)

Đúng(0)

Lê Mạnh Tiến Đạt

3 tháng 4 2017

Ta có ; \(\frac{1}{2009}+\frac{2}{2009}+\frac{3}{2009}+......+\frac{2008}{2009}\)

\(=\frac{1+2+3+......+2008}{2009}\)

\(=\frac{2017036}{2009}=1004\)

Đúng(0)

Bùi Thị Anh Thư

5 tháng 3 2017 - olm

\(\frac{56-x}{34}\)= \(\frac{144}{96}\)

Giúp nha cả cách làm và kết quả nhanh mik tick lun

#Toán lớp 5

viet

5 tháng 3 2017

x= 56 *96 / 34 * 144

x=5376/4896

Đúng(0)

Lan Phươnggg

5 tháng 3 2017

5 nha e

Đúng(0)

Mori Ran

15 tháng 4 2017 - olm

\(\frac{1}{2}+\frac{3}{22}\)

bạn nào làm nhanh và chính xác, mình sẽ tick nhưng các bạn phải tick cho mình

#Toán lớp 5

Nguyễn Huy Quân

15 tháng 4 2017

= 11/22 + 3/22 = 14/22

Đúng(0)

Mori Ran

15 tháng 4 2017

=\(\frac{7}{11}\)

k mình nha

chúc các bạn học giỏi

Đúng(0)

Lê Ngọc Ánh

23 tháng 6 2017 - olm

tính nhanh nhaD=\(\frac{3}{2x4}+\frac{3}{4x6}+...+\frac{3}{98x100}\)A=\(\frac{1}{2}+\frac{1}{3}+\frac{1}{6}+\frac{1}{12}\)B=\(6\frac{2}{3}+7\frac{5}{8}+3\frac{1}{3}+4\frac{5}{8}\)C=[\(4\frac{2}{5}+2\frac{3}{7}\)] - [\(2\frac{2}{5}-1\frac{4}{7}\)]E=\(\frac{131313}{151515}+\frac{131313}{353535}+\frac{131313}{636363}+\frac{131313}{999999}\)làm ơn giúp mik nhamik đang cần gấpmik sẽ tick(chắc chắn lun) cho người nhanh...

Đọc tiếp

#Toán lớp 5

Lê Hồng Nhung

23 tháng 6 2017

1/3xD=1/(2x4)+1/(4x6)+...+1/(98x100)
2/3xD=2/(2x4)+2/(4x6)+...+1/(98x100)
2/3xD= 1/2-1/4+1/4-1/6+...+1/98-1/100
2/3xD=1/2-1/100
2/3xD=49/100
D=147/200

Đúng(0)

Lê Hồng Nhung

23 tháng 6 2017

A=1/2+1/3+1/6+1/12
A=(1/2+1/3+1/6)+1/12
A=1+1/12
A=13/12

Đúng(0)

suni linh

1 tháng 5 2019 - olm

Tìm x:

\(\frac{4}{x}=\frac{1}{5}\)

Các bạn ghi rõ cách giải nha, ai làm đúng mik tích cho!!!

#Toán lớp 5

Serein

1 tháng 5 2019

Ta có:

\(\frac{4}{x}=\frac{1}{5}\)

\(\Rightarrow\frac{4}{x}=\frac{1.4}{5.4}=\frac{4}{20}\)

\(\Rightarrow x=20\)

Vậy \(x=20\)

~Study well~

Đúng(0)

ʚ๖ۣۜKɦáηɦ ๖ۣۜHυүềηɞ‏

1 tháng 5 2019

\(\frac{4}{x}=\frac{1}{5}\)

=> Ta thấy phân số có mẫu là x đã được rút gọn thành phân số \(\frac{1}{5}\)

=> x phải là một số tự nhiên khác 0 thỏa mãn phân số đã được rút gọn

Mà ta thấy : 4 : 4 = 1

Thế thì x : 4 = 5

=> x = 5 x 4 = 20

Vậy x = 20 thì thỏa mãn đề bài

Từ đó ta có : \(\frac{4}{20}=\frac{4:4}{20:4}=\frac{1}{5}\)

Đúng(0)

Phan Thảo Nguyên

3 tháng 1 2016 - olm

\(Đề=\frac{48}{a}=\frac{20}{35}\)
(Mik đang cần gấp.Bạn nào giải nhanh ,đúng là mik tick choa.Các bạn ghi đáp số rồi ghi cách giải sau nha)

#Toán lớp 5

Nguyễn Trung Hiếu

3 tháng 1 2016

Muốn tìm a ta lấy 48x35:20=84

Vậy a = 84

Đúng(0)

Minh Hiền

3 tháng 1 2016

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP