K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 1
a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Xét ΔABH vuông tại H và ΔKIH vuông tại H có
HA=HK
HB=HI
Do đó: ΔABH=ΔKIH
c: Xét ΔIAK có
IH là đường cao
IH là đường trung tuyến
Do đó: ΔIAK cân tại I
Ta có: ΔIAK cân tại I
mà IB là đường cao
nên IB là phân giác của góc AIK
d: Ta có: IA=IK
IA=ID
Do đó: IK=ID=DA/2
Ta có: ID=IA
I nằm giữa D và A
Do đó: I là trung điểm của DA
Xét ΔDKA có
KI là đường trung tuyến
\(KI=\dfrac{DA}{2}\)
Do đó: ΔKDA vuông tại K
15 tháng 5 2022
a: để y>0 thì 2a-1<0
hay a<1/2
b: Để y<0 thì 2a-1>0
hay a>1/2
15 tháng 5 2022
c) Để y ko là số dương của ko là số âm thì:
\(y=\dfrac{2a-1}{-3}=0\Rightarrow2a-1=0\Rightarrow a=\dfrac{1}{2}\)
25 tháng 5 2022
\(\Leftrightarrow\left(x+1\right)\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
=>x+1=0
hay x=-1
TC
25 tháng 5 2022
\(\Leftrightarrow\left(x+1\right).\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}\right)=\left(x+1\right)\left(\dfrac{1}{13}+\dfrac{1}{14}\right)\)
\(\Leftrightarrow\left(x+1\right)\left(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\right)=0\)
mà \(\dfrac{1}{10}+\dfrac{1}{11}+\dfrac{1}{12}-\dfrac{1}{13}-\dfrac{1}{14}\ne0\)
\(=>x+1=0\Leftrightarrow x=-1\)
KT
ÉT Ô ÉT
Câu 3: Tìm x biết:
|x + 1| + |x + 2| + |x + 2020| = 4x
Giúp mik với!!!
Mik hứa Tick cho… Pls
2
22 tháng 4 2023
TH1 : \(x< -2020\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) - ( x + 2020 ) = 4x
<=> -3x - 2023 = 4x <=> -7x = 2023 <=> x = -289
TH2 : \(-2020\le x< -2\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) - ( x + 2 ) + x + 2020 = 4x
<=> -x + 2017 = 4x
<=> -5x = -2017 <=> x = 2017/5 ( = 403,4 )
TH3 : \(-2\le x< -1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = - ( x + 1 ) + x + 2 + x + 2020 = 4x
<=> x + 2021 = 4x <=> -3x = -2021 <=> x = 2021/3
TH4 : \(x>-1\)
<=> | x + 1 | + | x + 2 | + | x + 2020 | = x + 1 + x + 2 + x + 2020 = 4x
<=> 3x + 2023 = 4x
<=> -x = -2023 <=> x = 2023
Vậy...
22 tháng 4 2023
TH1: x ≥ 0
Khi đó \(\left|x+1\right|+\left|x+2\right|+\left|x+2020\right|=x+1+x+2+x+2020\)
\(=3x+2023=4x\)
Suy ra \(4x-3x=x=2023\) (thỏa mãn điều kiện)
TH2: x < 0
Khi đó 4x < 0 hay vế phải luôn là một số âm. Tuy nhiên vế trái luôn luôn có giá trị lớn hơn 0 nên luôn là 0 hoặc là một số dương, suy ra vô lí.
Tóm lại, x = 2023.
4 tháng 4 2022
Áp dụng tính chất dãy tỉ số bằng nhau:\(\dfrac{\left(5z-3y\right)+\left(3x-2z\right)+\left(2y-5x\right)}{2+5+3}\)
=\(\dfrac{\left(3x-5x\right)+\left(-3y+2y\right)+\left(5z-2z\right)}{2+5+3}\)
=\(\dfrac{-2x-y+3z}{2+5+3}\)(???!!!!)
=\(\dfrac{-2x}{2}=\dfrac{-y}{5}=\dfrac{3z}{3}\)
=\(\dfrac{2}{-2x}=\dfrac{5}{-y}=\dfrac{3}{3z}\)
tớ xin chịu trận vì ko chứng minh được :(((
nó lại ra như thế này
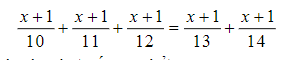
a, \(3\left(x-3\right)^2+\left(y-1\right)^2+2005\ge2005\)
Dấu ''='' xảy ra khi x = 3 ; y = 1
b, \(\left|x^2-1\right|+\left(x-1\right)^2+y^2+12\ge12\)
Dấu ''='' xảy ra khi x = 1 ; y = 0
c, Ta có \(\left(2x-3\right)^2+5\ge5\Rightarrow\dfrac{4}{\left(2x-3\right)^2+5}\le\dfrac{4}{5}\Rightarrow C\ge-\dfrac{4}{5}\)
Dấu ''='' xảy ra khi x = 3/2