Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đ á p á n C T h e o g i ả t h i ế t : X l à e s t e n o , m ạ c h h ở c ó 4 n g u y ê n t ử C , t ạ o b ở i a x i t v à a n c o l . S u y r a X c ó t h ể l à e s t e n o đ ơ n c h ứ c , h o ặ c e s t e n o , h a i c h ứ c - E s t e n o , đ ơ n c h ứ c C 4 H 8 O 2 : H C O O C H C H 3 2 H C O O C H 2 C H 3 C H 3 C O O C 2 H 5 C 2 H 5 C O O C H 3 - E s t e n o , h a i c h ứ c C 4 H 6 O 4 : C H 3 O O C - C O O C H 3 H C O O C H 2 - C H 2 O O C H .

Chọn đáp án B
Đốt X cho nCO2 = nO2 Þ X có dạng Cn(H2O)m hay số H = 2 số O Þ Loại đáp án A và C
x mol X thủy phân tạo 2x mol ancol
Þ X tạo ra từ axit 2 chức và ancol đơn chức Þ Loại đáp án D.

Đáp án D
Độ bất bão hòa: k = (2C + 2 – H):2 = (2.6+2-10):2 = 2
Mà thủy phân hoàn toàn X trong môi trường axit thu được axit cacboxylic Y duy nhất và hỗn hợp chứa 2 ancol
=> X là este no, 2 chức, mạch hở => Y là axit no 2 chức, mạch hở
CTCT của X:
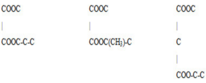
Vậy có 3 CTCT phù hợp

Các bạn chú ý, khi tính ra E(\(\pi\)) = 1,7085.10-18 thì đơn vị là J2s2/kg.m2 chứ không phải là đơn vị (J), sau đó nhân với NA và nhân với 10-3 thì mới ra được kết quả là 1,06.103 kJ/mol.
bạn có ghi bài trên lớp phần cấu tạo chất đủ không. co mình mượn chép lại mấy bài phần đó với

(mol) ;
(mol).
(mol) => m = 0,02.304 = 6,08 (gam).
X là C17H31COOC3H5(C17H33COO)2 ; nX = nglixerol = 0,01 mol
=> a = 0,01.882 = 8,82 (gam)

phương trình dạng toán tử : \(\widehat{H}\)\(\Psi\) = E\(\Psi\)
Toán tử Laplace: \(\bigtriangledown\)2 = \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\)
thay vào từng bài cụ thể ta có :
a.sin(x+y+z)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))sin(x+y+z)
=\(\frac{\partial^2}{\partial x^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial y^2}\)sin(x+y+z) + \(\frac{\partial^2}{\partial z^2}\)sin(x+y+z)
=\(\frac{\partial}{\partial x}\)cos(x+y+z) + \(\frac{\partial}{\partial y}\)cos(x+y+z) + \(\frac{\partial}{\partial z}\)cos(x+y+z)
= -3.sin(x+y+z)
\(\Rightarrow\) sin(x+y+z) là hàm riêng. với trị riêng bằng -3.
b.cos(xy+yz+zx)
\(\bigtriangledown\)2 f(x,y,z) = ( \(\frac{\partial^2}{\partial x^2}\)+ \(\frac{\partial^2}{\partial y^2}\)+\(\frac{\partial^2}{\partial z^2}\))cos(xy+yz+zx)
=\(\frac{\partial^2}{\partial x^2}\)cos(xy+yz+zx) +\(\frac{\partial^2}{\partial y^2}\)cos(xy+yz+zx) + \(\frac{\partial^2}{\partial z^2}\)cos(xy+yz+zx)
=\(\frac{\partial}{\partial x}\)(y+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial y}\)(x+z).-sin(xy+yz+zx) + \(\frac{\partial}{\partial z}\)(y+x).-sin(xy+yz+zx)
=- ((y+z)2cos(xy+yz+zx) + (x+z)2cos(xy+yz+zx) + (y+x)2cos(xy+yz+zx))
=-((y+z)2+ (x+z)2 + (x+z)2).cos(xy+yz+zx)
\(\Rightarrow\) cos(xy+yz+zx) không là hàm riêng của toán tử laplace.
c.exp(x2+y2+z2)


Đáp án C
6