
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`(4\sqrt{6}+x)^2=8^2+(6+\sqrt{x^2+4})^2`
`<=>96+8\sqrt{6}x+x^2=64+36+12\sqrt{x^2+4}+x^2+4`
`<=>2\sqrt{6}x-2=3\sqrt{x^2+4}` `ĐK: x >= \sqrt{6}/6`
`<=>24x^2-8\sqrt{6}x+4=9x^2+36`
`<=>15x^2-8\sqrt{6}x-32=0`
`<=>x^2-[8\sqrt{6}]/15x-32/15=0`
`<=>(x-[4\sqrt{6}]/15)^2-64/25=0`
`<=>|x-[4\sqrt{6}]/15|=8/5`
`<=>[(x=[24+4\sqrt{6}]/15 (t//m)),(x=[-24+4\sqrt{6}]/15(ko t//m)):}`

a.
\(\Delta=\left(-5\right)^2-4.3.2=25-24=1>0\)
\(\Rightarrow\) Phương trình có 2 nghiệm pb
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{5}{3}\\x_1x_2=\dfrac{2}{3}\end{matrix}\right.\)
\(4A=x_1^2+x_2^2-x_1x_2=\left(x_1^2+x_2^2+2x_1x_2\right)-3x_1x_2\)
\(4A=\left(x_1+x_2\right)^2-3x_1x_2\)
\(4A=\left(\dfrac{5}{3}\right)^2-3.\left(\dfrac{2}{3}\right)=\dfrac{7}{9}\)
\(\Rightarrow A=\dfrac{7}{36}\)

Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$

a)Xét ΔABC cân tại A có AE là trung tuyến
⇒ AE cũng là đường cao của ΔABC
⇒ AE⊥BC \(\Rightarrow\widehat{AEB}=\widehat{AEC}=90^o\)
Xét tứ giác ADBE có \(\widehat{ADB}\) và \(\widehat{AEB}\) cùng nhìn AB dưới góc 90o
⇒ ADBE là tứ giác nội tiếp
⇒ 4 điểm A,D,B,E cùng thuộc (O)
b) Vì BD⊥AC hay HD⊥AC ⇒ ΔHDC vuông tại D
⇒ Tâm của đường tròn đi qua 3 điểm H,D,C là trung điểm của HC
hay I là trung điểm của HC
c) Xét tứ giác HDCE có 2 góc đối \(\widehat{HDC}+\widehat{HEC}=90^o+90^o=180^o\)
⇒ HDCE là tứ giác nội tiếp
⇒ 2 điểm H,E thuộc (I)
Mà 2 điểm H,E cũng thuộc (O)
⇒ Đường tròn tâm O và đường tròn tâm I có 2 điểm chung
a: Ta có: ΔABC cân tại A
mà AE là đường trung tuyến ứng với cạnh đáy BC
nên AE là đường cao ứng với cạnh BC
Xét tứ giác ADEB có
\(\widehat{ADB}=\widehat{AEB}=90^0\)
Do đó: ADEB là tứ giác nội tiếp
hay A,D,E,B cùng thuộc 1 đường tròn

\(\left\{{}\begin{matrix}3x-2y=-2\\2x+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=-2\\4x+2y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=0\\2x+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2.0+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\0+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Vậy...
\(\left\{{}\begin{matrix}3x-2y=-2\\2x+y=1\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}3x-2y=-2\\4x+2y=2\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}7x=0\\2x+y=1\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=0\\2.0+y=1\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
vậy...


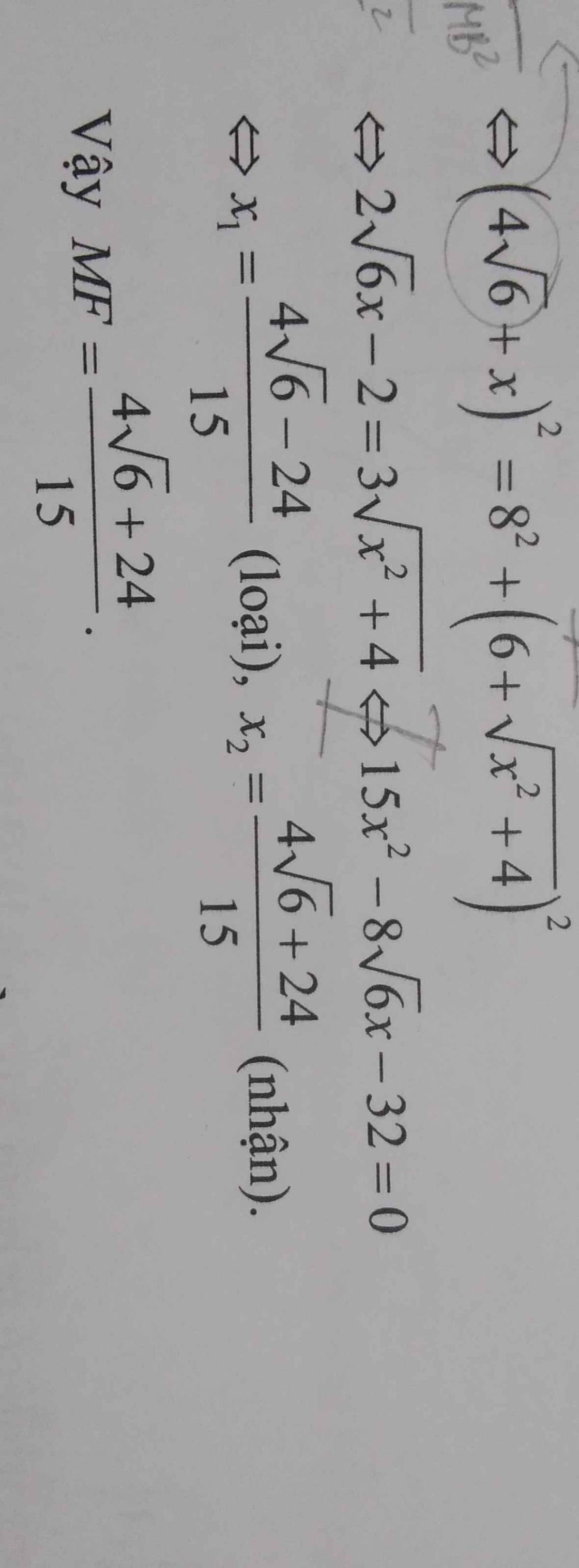
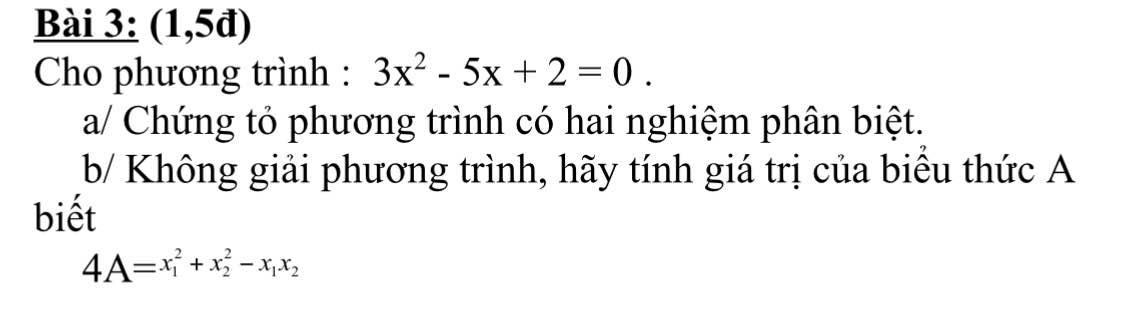
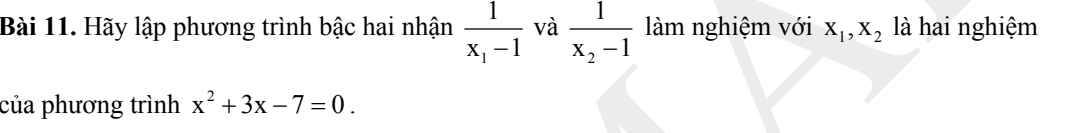


Mà e đâu cs thấy ảnh của a đăng lên
ý là đăng hình vẽ phải ko ạ? Nếu muốn vẽ hình thì nhấn vô cái biểu tượng "hình vuông và tam giác ý" nó tên vẽ hình trực tuyến. Còn nếu muốn đăng ảnh, vd anime thì hk có đăng đc đâu