
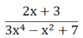
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

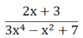

Muốn rút gọn phân thức đại số ta có thể :
+ Phân tích tử và mẫu thành nhân tử ( nếu cần ) để tìm nhân tử chung.
+ Chia cả tử và mẫu cho nhân tử chung.
Rút gọn phân thức :
\(\dfrac{8x-4}{8x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{2x^3-1}\)\(=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(2x^2+2x+1\right)}\)\(=\dfrac{4}{4x^2+2x+1}\)
*Quy tắc rút gọn một phân thức đại số là:
-Phân tích tử và mẫu thành nhân tử (nếu cần) để tìm nhân tử chung.
-Chia cả tử và mẫu cho nhân tử chung.
*Bài tập:
\(\dfrac{8x-4}{8x^3-1}=\dfrac{4\left(2x-1\right)}{\left(2x-1\right)\left(x^2+x+1\right)}=\dfrac{4}{x^2+x+1}\)

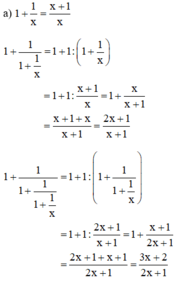
b) + Dự đoán :
Quy luật : Giả sử viết các phân thức trên thành một dãy thì phân thức sau có tử bằng tổng của tử và mẫu của phân thức đứng liền trước và mẫu bằng tử của phân thức đứng liền trước đó.
Do đó :
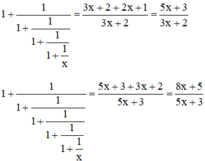
+ Kiểm chứng :
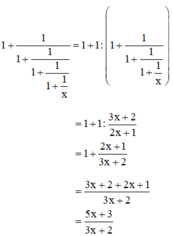
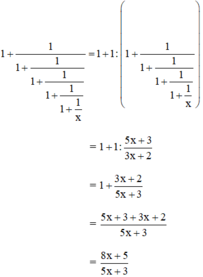

\(\frac{x+\frac{1}{y}}{y+\frac{1}{x}}=\frac{\frac{xy}{y}}{\frac{xy}{x}}=\frac{xy}{y}.\frac{x}{xy}=\frac{x}{y}\)
\(\frac{x+\frac{1}{y}}{y+\frac{1}{x}}=\left(x+\frac{1}{y}\right):\left(y+\frac{1}{x}\right)=\frac{xy+1}{y}:\frac{xy+1}{x}=\frac{\left(xy+1\right)\cdot x}{\left(xy+1\right)\cdot y}=\frac{x}{y}\).

a)+1+1x=xx+1x=x+1x1+1x=xx+1x=x+1x
Áp dụng câu a) ta có :
1+11+1x=1+1x+1x=1+xx+1=x+1+x1+x=2x+1x+11+11+1x=1+1x+1x=1+xx+1=x+1+x1+x=2x+1x+1
Dùng kết quả câu b) ta có :
1+11+11+1x=1+12x+1x+1=1+x+12x+1=2x+1+x+12x+1=3x+22x+11+11+11+1x=1+12x+1x+1=1+x+12x+1=2x+1+x+12x+1=3x+22x+1
b)Đối với các biểu thức có dạng đã cho có thể dự đoán như sau :
Qua các kết quả của các bài ở câu a ta thấy kết quả tiếp theo sau là một phân thức mà tử bằng tổng của tử và mẫu, còn mẫu là tử của kết quả vế trước đó.
Như vậy có thể dự đoán rằng nếu biểu thức có 4 gạch phân số thì kết quả là 5x+33x+25x+33x+2, và trong trường hợp này có 5 gạch phân số, kết quả sẽ là 8x+55x+38x+55x+3 .
Thật vậy : 1+11+11+11+11+1x=1+13x+22x+1=1+2x+13x+2=3x+2+2x+13x+2=5x+33x+21+11+11+11+11+1x=1+13x+22x+1=1+2x+13x+2=3x+2+2x+13x+2=5x+33x+2
Do đó 1+11+11+11+11+1x=1+15x+33x+21+11+11+11+11+1x=1+15x+33x+2

Thông báo thay trang thay mặt người phân phối chương trình xin tặng chương trình học online số 1 Việt Nam. Sự kiện bắt đầu từ ngày 28/10 đến 1/11
Xin chào các thành viên đang online trên trang. Sự kiện khuyến mãi được tài trợ 500 suất áo chiếc áo đá bóng Việt Nam.Mong tất cả mọi người đã xem vào truy cập sau để nhận thưởng khi xem có 1 bản đăng kí nhận miễn phí : Thời gian có hạn tặng mọi người đã tham gia tích cực -> Không tin các bạn có thể hỏi các CTV nha mình chỉ có quyền thông báo :
Copy cái này hoặc gõ :
https://lazi.vn/quiz/d/16491/nhac-edm-la-loai-nhac-the-loai-gi
--

a)Ta có:
3x2−4x−17x+2=3x−10+3x+23x2−4x−17x+2=3x−10+3x+2
Để phân thức là số nguyên thì 3x+23x+2 phải là số nguyên (với giá trị nguyên của x).
3x+23x+2 nguyên thì x +2 phải là ước của 3.
Các ước của 3 là ±1,±3±1,±3 . Do đó
x+2=±1=>x=−1,x=−3x+2=±1=>x=−1,x=−3
x+2=±3=>x=1,x=−5x+2=±3=>x=1,x=−5
Vậy x=−5;−3;−1;1.x=−5;−3;−1;1.
Cách khác:
3x2−4x−17x+2=(3x2+6x)−(10x+20)+3x+23x2−4x−17x+2=(3x2+6x)−(10x+20)+3x+2
=3x(