Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tập hợp các số nguyên Z nằm trong tập hợp các số hữu tỉ Q
Có thể nói mỗi số nguyên là một số hữu tỉ

a)
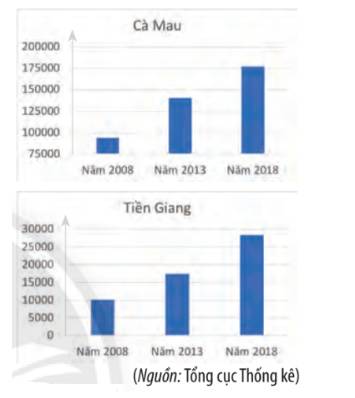
Phát biểu i sai vì ở Tiền Giang sản lượng các năm đều nhỏ hơn 30 000 tấn, còn ở Cà Mau sản lượng các năm đều lớn hơn 75 000 tấn.
Phát biểu ii sai do sản lượng nuôi tôm ở Cà Mau năm 2018 là 175 000 tấn gấp gần 2 lần năm 2008 là 95 000 tấn.
Phát biểu iii đúng do sản lượng nuôi tôm ở Tiền Giang năm 2018 là 28 500 tấn gấp hơn 2,5 lần năm 2008 là 10 000 tấn.
Phát biểu iv đúng do sản lượng nuôi tôm ở Tiền Giang năm 2008 là 10000 tấn, năm 2013 là 17 500 tấn và năm 2018 là 28 500 tấn, đều tăng trên 50% so với năm cũ.
Phát biểu v sai do từ năm 2013 đến 2018, tỉnh Cà Mau tăng 175 000 – 140 000 = 35 000 tấn, tương ứng 25% còn tỉnh Tiền Giang, tăng (28 500 – 17 500) : 17 500 = 63%
b)
Để so sánh sản lượng nuôi tôm của hai tỉnh Cà Mau và Tiền Giang, ta nên sử dụng loại biểu đồ cột kép.

Nhìn vào biểu đồ ta thấy giá trị sản phẩm trung bình thu được trên một hecta mặt nước nuôi trồng thủy sản đều cao hơn trên một hecta đất trồng trọt nên khẳng định ở câu a) là đúng.
Dễ thấy giá trị sản phẩm trung bình thu được trên một hecta mặt nước nuôi trồng thủy sản (hoặc đất trồng trọt) đều có xu hướng tăng từ năm 2014 đến năm 2018. Do đó, khẳng định ở câu b2,3) là đúng.
Từ năm 2014 đến năm 2018, giá trị sản phẩm trung bình thu được trên một hecta đất trồng trọt tăng từ khoảng 80 đến 95, trong khi trên một hecta mặt nước nuôi trồng thủy sản là từ gần 180 đến 225, gấp cao gấp khoảng 2,3 lần. Do đó khẳng định ở câu c) là sai.

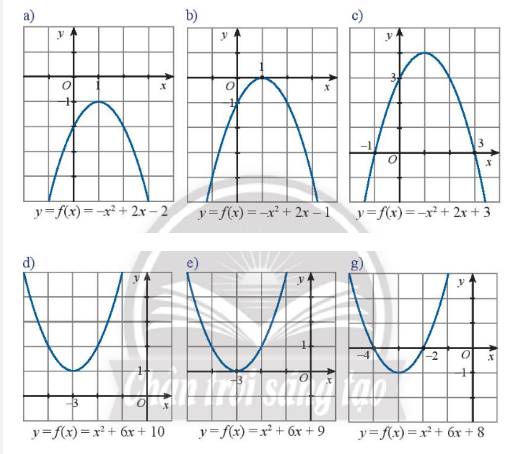
a) Dựa vào đồ thị ta thấy hàm số đã cho vô nghiệm
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 2} \right) = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
b) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = 1\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 1} \right) = 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với \(\forall x \in \mathbb{R}\)
c) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 1;{x_2} = 3\)
Biệt thức \(\Delta = {2^2} - 4.\left( { - 1} \right).3 = 16 > 0\)
Ta thấy hệ số của \({x^2}\) là \( - 1 < 0\)
Đồ thị nằm dưới trục hoành khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
Đồ thị nằm trên trục hoành với mọi \(x \in \left( { - 1,3} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 1} \right) \cup \left( {3, + \infty } \right)\)
d) Dựa vào đồ thị ta thấy hàm số bậc hai đã cho vô nghiệm
Biệt thức \(\Delta = {6^2} - 4.1.10 = - 4 < 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi \(x\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
e) Dựa vào đồ thị ta thấy hàm số đã cho có nghiệm kép \({x_1} = {x_2} = - 3\)
Biệt thức \(\Delta = {6^2} - 4.1.9 = 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành với mọi x
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) với mọi \(x \in \mathbb{R}\)
g) ) Dựa vào đồ thị ta thấy hàm số đã cho có hai nghiệm phân biệt \({x_1} = - 4;{x_2} = - 2\)
Biệt thức \(\Delta = {6^2} - 4.1.8 = 4 > 0\)
Ta thấy hệ số của \({x^2}\) là \(1 > 0\)
Đồ thị nằm trên trục hoành khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)
Đồ thị nằm dưới trục hoành với mọi \(x \in \left( { - 4, - 2} \right)\)
Nên \(f\left( x \right)\) cùng dấu với hệ số của \({x^2}\) khi \(x \in \left( { - \infty , - 4} \right) \cup \left( { - 2, + \infty } \right)\)

Tham khảo:
Ta có:
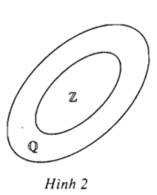
Mỗi hình chữ nhật là một hình bình hành đặc biệt (có một góc vuông). Do đó: \(C \subset B\)
Mỗi hình thoi là một hình bình hành đặc biệt (có hai cạnh kề bằng nhau). Do đó: \(E \subset B\)
Mỗi hình bình hành là một hình tứ giác (có một cặp cạnh đối song song và bằng nhau). Do đó: \(B \subset A\)
\(C \cap E\)là tập hợp các hình vừa là hình chữ nhật vừa là hình thoi, hay là hình chữ nhật có 4 cạnh bằng nhau (hình vuông). Do đó: \(C \cap E = D\)
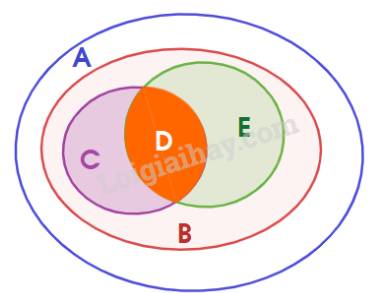
Kết hợp lại ta có: \(\left\{ \begin{array}{l}D \subset C \subset B \subset A,\\D \subset E \subset B \subset A,\\C \cap E = D\end{array} \right.\)
Biểu đồ Ven:

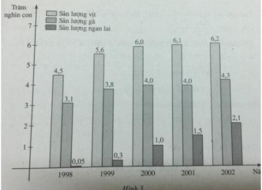
Tập xác định của cả ba hàm số y = f(x), y = g(x) và y = h(x) là:
D = {1998, 1999, 2000, 2001, 2002}

| Lớp của khối lượng | Tần số | Tần suất |
| [70; 80) | 3 | 10% |
| [80; 90) | 6 | 20% |
| [90; 100) | 12 | 40% |
| [100; 110) | 6 | 20% |
| [110; 120) | 3 | 10% |
| Cộng | 30 | 100% |
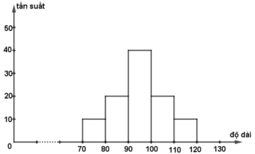
a) Biểu đồ tần suất hình cột:
Biểu đồ tần suất hình gấp khúc:
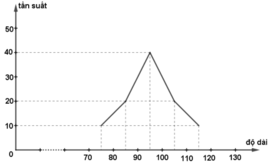
b) Biểu đồ tần số hình cột:
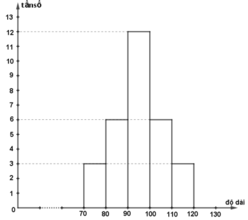
Biểu đồ tần số đường gấp khúc:
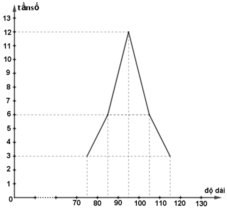
c) Dựa vào biểu đồ tần suất hình cột ta nhận thấy khối lương khoai tây thường nằm trong khoảng từ 90 đến 100 gram.

a) Biểu đồ tần suất hình cột và đường gấp khúc tần suất như sau:
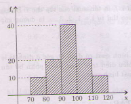

Biểu đồ tần suất hình cột Đường gấp khúc tần suất
b) Chú ý rằng trong biểu đồ tần suất cũng như biểu đồ tần số hình cột, hay đường gấp khúc tần suất, đường gấp khúc tần số thì đơn vị đo dài ở hai trục không nhất thiết phải bằng nhau. Vì vậy có thể dùng chính biểu đồ tần suất làm biểu đồ tần số hình cột, miễn là thay chứ f ở trục đứng bằng n, các số chỉ tần suất được thay bằng tần số tương ứng. Cụ thể ở hình trên thế f bởi n, thế 40 bởi 12, thế 20 bởi 6 thế 10 bởi 3. cũng làm như vậy trong hình đường gấp khúc tần suất, ta có đường gấp khúc theo tần số.
c) Theo hình trong câu a) ta thấy phần lớn các củ khoai được khảo sát (80%) có khối lượng từ 80 gam đến 110 gam, 40% số củ khoai có khối lượng từ 90 đến 100 gam.

f(2002) = 620000 (con)
g(1999) = 380000 (con)
h(2000) = 100000 (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.