
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




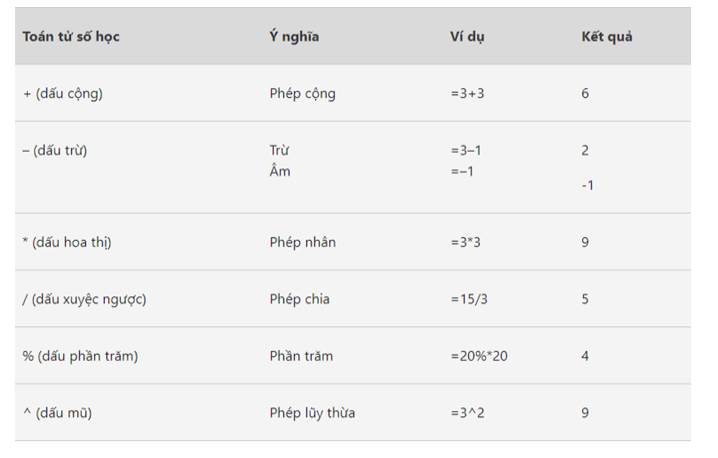
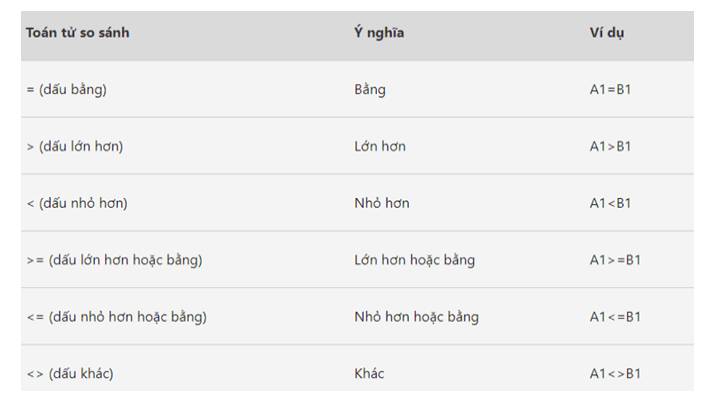
Phép gán được sử dụng để gán giá trị cho một biến trong lập trình. Trong mã giả, phép gán được viết bằng dấu bằng "=", với biến ở bên trái dấu bằng và giá trị muốn gán ở bên phải. Dấu bằng "=" trong mã giả chỉ thực hiện phép gán giá trị cho biến, không phải là một mệnh đề so sánh.

Tham khảo:
Viết chương trình Python thực hiện thuật toán sắp xếp chèn tuyến tính dựa trên mã giả đã cho trong báo học:
void Insertion_Sort(int a[], int n){
int pos, i;
int x;//lưu giá trị a[i] tránh bị ghi đè khi dời chỗ các phần tử
for(i=1; i<n; i++){//đoạn a[0] đã sắp xếp
x = a[i]; pos = i-1;
//tìm vị trí chèn x
while((pos>=0)&&(a[pos]>x)){
//kết hợp dời chỗ các phần tử sẽ đứng sau x trong danh sách mới
a[pos+1] = a[pos];
pos--;
}
a[pos+1] = x;//chèn x vào danh sách
}
}
void main()
{
int a[5] = {8, 4, 1, 6, 5};
Insertion_Sort(a, 5);
cout<<"Mang sau khi sap xep:"<<endl;
for(int i=0;i<5;i++){
cout<<a[i]<<" ";
}
system("pause");


Sau lần chia đôi đầu tiên, pham vi tìm kiếm còn lại n/2 số, sau khi chia đôi lần thứ hai, dãy còn lại n/4 số, sau khi chia đôi lần thứ dãy còn lại n/8, …sau khi chia đôi lần k dãy còn lại n/2.mũ k. Kết thúc khi 2 mũ k sấp xỉ n.

1. Google Drive là dịch vụ lưu trữ trực tuyến của Google, với dung lượng ban đầu được miễn phí tới 15GB, người dùng sẽ thoải mái lưu lại những bức ảnh, văn bản, hay bài viết của mình lên "đám mây". Nhờ được tích hợp với Gmail, Google Docs và Google+, người dùng Google Drive có thể dễ dàng truy cập, xử lý thông tin hay sử dụng những dữ liệu này ở bất kỳ đâu, bất cứ lúc nào, với bất kỳ ai. Ngoài ra, những dữ liệu bị xóa (cố tình hay vô tình) đều sẽ được lưu lại trong thùng rác chứ không mất đi ngay lập tức.
2. Dropbox Tuy dung lượng miễn phí ban đầu không bằng Google (chỉ có 2GB), nhưng Dropbox lại là dịch vụ khá ổn định và được lựa chọn sử dụng khá nhiều. Không có bất cứ yêu cầu nào về định dạng, dung lượng file cho vào lưu trữ, Dropbox không chỉ là dịch vụ được yêu thích nhất, có mặt trên nhiều hệ điều hành nhất, mà còn là một trong những dịch vụ có tuổi đời cao nhất trên thị trường này.

1. Sắp xếp chèn (Insertion Sort)
Ý tưởng: Insertion Sort lấy ý tưởng từ việc chơi bài, dựa theo cách người chơi "chèn" thêm một quân bài mới vào bộ bài đã được sắp xếp trên tay.
2. Sắp xếp lựa chọn (Selection Sort)
Ý tưởng của Selection sort là tìm từng phần tử cho mỗi vị trí của mảng hoán vị A' cần tìm.
3. Sắp xếp nổi bọt (Bubble Sort)
Ý tưởng: Bubble Sort, như cái tên của nó, là thuật toán đẩy phần tử lớn nhất xuống cuối dãy, đồng thời những phần tử có giá trị nhỏ hơn sẽ dịch chuyển dần về đầu dãy. Tựa như sự nổi bọt vậy, những phần tử nhẹ hơn sẽ nổi lên trên và ngược lại, những phần tử lớn hơn sẽ chìm xuống dưới.

Đọc mã lệnh của thuật toán Eratosthenes cho ở Hình 5 và mô tả liệt kê các bước của thuật toán và bằng mã giả:
Đục bỏ dần các số không nguyên tố bằng cách đánh dấu “là hợp số” (không phải số nguyên tố) mỗi khi biết số đó là bội số của một số nguyên tố.

Ví dụ:
int number = 1990;if ((number % 2) == 0)Console.WriteLine($"{number} là số chẵn");// In ra: 1990 là số chẵnint a = 5;int b = 10;if (a >= b){Console.WriteLine("Số a lớn hơn hoặc bằng số b");}else{Console.WriteLine("Số a nhỏ hơn số b");}//In ra: Số a nhỏ hơn số b
Sau else bạn có thể bắt đầu ngay một lệnh if khác để tạo ra cấu trúc if else, kiểm tra nhiều trường hợp
int a = 10;int b = 10;if (a > b){Console.WriteLine("Số a lớn hơn hoặc bằng số b");}else if (a < b){Console.WriteLine("Số a nhỏ hơn số b");}else{Console.WriteLine("Hai số a, b bằng nhau");}pan>Console.WriteLine("Hai số a, b bằng nhau");}
Trong bài toán sắp xếp dãy số, ta cần phải sắp xếp các số trong dãy theo một thứ tự tăng dần hoặc giảm dần. Để giảm số lần so sánh và hoán vị giữa các phần tử trong quá trình sắp xếp, ta cần chọn phương pháp sắp xếp phù hợp. Trường hợp thuận lợi nhất trong bài toán sắp xếp dãy số là khi dãy đã có thứ tự tăng dần hoặc giảm dần.
Trong trường hợp này, ta không cần phải hoán vị các phần tử trong quá trình sắp xếp, do đó số phép toán cần làm là ít nhất.
Ngược lại, khi dãy số ban đầu là một dãy không có thứ tự, ta cần thực hiện một số lần hoán vị để sắp xếp dãy theo thứ tự mong muốn. Trong trường hợp này, số phép toán cần làm sẽ nhiều hơn so với trường hợp dãy đã có thứ tự. Do đó, để có trường hợp thuận lợi nhất và số phép toán cần làm ít nhất, ta nên sắp xếp dãy số theo thứ tự tăng dần hoặc giảm dần trước khi thực hiện các phép toán sắp xếp khác.