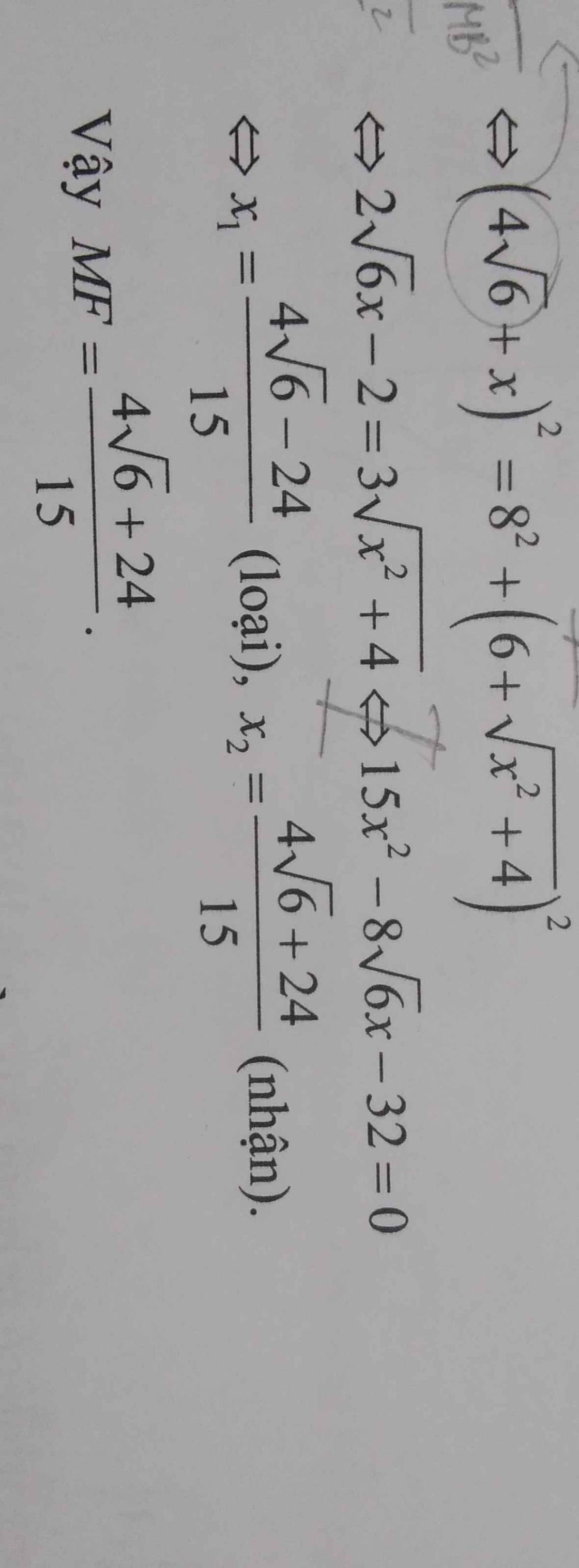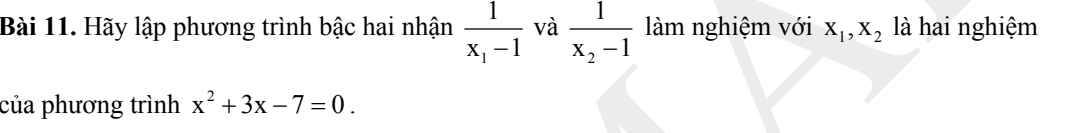Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`(4\sqrt{6}+x)^2=8^2+(6+\sqrt{x^2+4})^2`
`<=>96+8\sqrt{6}x+x^2=64+36+12\sqrt{x^2+4}+x^2+4`
`<=>2\sqrt{6}x-2=3\sqrt{x^2+4}` `ĐK: x >= \sqrt{6}/6`
`<=>24x^2-8\sqrt{6}x+4=9x^2+36`
`<=>15x^2-8\sqrt{6}x-32=0`
`<=>x^2-[8\sqrt{6}]/15x-32/15=0`
`<=>(x-[4\sqrt{6}]/15)^2-64/25=0`
`<=>|x-[4\sqrt{6}]/15|=8/5`
`<=>[(x=[24+4\sqrt{6}]/15 (t//m)),(x=[-24+4\sqrt{6}]/15(ko t//m)):}`

Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$
Lời giải:
Áp dụng định lý Viet đối với pt $x^2+3x-7=0$ ta có:
$x_1+x_2=-3$
$x_1x_2=-7$
Khi đó:
$\frac{1}{x_1-1}+\frac{1}{x_2-1}=\frac{x_2-1+x_1-1}{(x_1-1)(x_2-1)}$
$=\frac{(x_1+x_2)-2}{x_1x_2-(x_1+x_2)+1}=\frac{-3-2}{-7-(-3)+1}=\frac{5}{3}$
$\frac{1}{x_1-1}.\frac{1}{x_2-1}=\frac{1}{(x_1-1)(x_2-1)}=\frac{1}{x_1x_2-(x_1+x_2)+1}=\frac{1}{-7-(-3)+1}=\frac{-1}{3}$
Khi đó áp dụng định lý Viet đảo, $\frac{1}{x_1-1}, \frac{1}{x_2-1}$ là nghiệm của pt:
$x^2-\frac{5}{3}x-\frac{1}{3}=0$

Có \(a^2+b^2=3-ab\)
Mà \(a^2+b^2\ge2ab\)
\(\Leftrightarrow3\ge3ab\)
\(\Leftrightarrow1\ge ab\left(1\right)\)
Cũng có:\(a^2+b^2\ge-2ab\)
\(\Leftrightarrow3-ab\ge-2ab\)
\(\Leftrightarrow-3\le ab\left(2\right)\)
Từ (1) và (2) \(1\ge ab\ge-3\)
Lại có :
\(\left(a^2+b^2\right)^2=\left(3-ab\right)^2\)
\(\Leftrightarrow a^4+b^4=9-6ab+a^2b^2-2a^2b^2=9-6ab-a^2b^2\)
\(\Rightarrow P=a^4+b^4-ab=9-7ab-a^2b^2=-\left(a^2b^2+7ab-9\right)\)
\(\Leftrightarrow P=-\left(a^2b^2-7ab+8ab\right)\)
\(\Leftrightarrow P=\left(ab+3\right)\left(-ab-4\right)+21\)
Có \(ab\ge-3\Rightarrow ab+3\ge0\)
\(-ab-4< 0\)
\(\Rightarrow P\le21\)
Max P = 21<=> ab=-3;a=-b<=>\(b=\pm\sqrt{3};a=\pm\sqrt{3}\)tương ứng

Bài 4:
\(a,A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\\ P=A:B=\dfrac{\sqrt{x}+1}{\sqrt{x}}\cdot\dfrac{x-1}{\sqrt{x}+1}=\dfrac{x-1}{\sqrt{x}}\\ b,P\sqrt{x}=m-\sqrt{x}+x\\ \Leftrightarrow x-1=m-\sqrt{x}+x\\ \Leftrightarrow m=\sqrt{x}-1\)

Bạn cứ đăng bài lên trên đây để mọi người giải đáp giúp cho.

Bài 1:
ĐKXĐ: \(x\ge\dfrac{1}{2}\)
Ta có: \(\sqrt{5x^2}=2x-1\)
\(\Leftrightarrow5x^2=\left(2x-1\right)^2\)
\(\Leftrightarrow5x^2-4x^2+4x-1=0\)
\(\Leftrightarrow x^2+4x-1=0\)
\(\text{Δ}=4^2-4\cdot1\cdot\left(-1\right)=20\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-4-2\sqrt{5}}{2}=-2-\sqrt{5}\left(loại\right)\\x_2=\dfrac{-4+2\sqrt{5}}{2}=-2+\sqrt{5}\left(loại\right)\end{matrix}\right.\)
Bài 1: Bình phương hai vế lên có giải ra được kết quả. Nhưng phải kèm thêm điều kiện $2x-1\geq 0$ do $\sqrt{5x^2}\geq 0$
PT \(\Leftrightarrow \left\{\begin{matrix} 2x-1\geq 0\\ 5x^2=(2x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x^2+4x-1=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2)^2-5=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ (x+2-\sqrt{5})(x+2+\sqrt{5})=0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} x\geq \frac{1}{2}\\ x=-2\pm \sqrt{5}\end{matrix}\right.\) (vô lý)
Vậy pt vô nghiệm.

Câu 2:
Ta có: \(\sqrt{x^2-4x+4}=x-1\)
\(\Leftrightarrow2-x=x-1\left(x< 2\right)\)
\(\Leftrightarrow-2x=-3\)
hay \(x=\dfrac{3}{2}\left(tm\right)\)