Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Dựa vào đáp án, ta thấy rằng
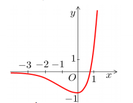
(1) Đường thẳng f x = 0 ⇔ 3 2 x - 2 . 3 x = 0 ⇔ 3 x = 2 ⇔ x = log 3 2 ⇒ 1 đúng.
(2) Bất phương trình f x ≥ - 1 ⇔ 3 2 x - 2 . 3 x + 1 ≥ 0 ⇔ 3 x - 1 2 ≥ 0 , ∀ x ∈ ℝ . Nên f x ≥ - 1 có vô số nghiệm ⇒ 2 sai.
(3) Bất phương trình f x ≥ 0 ⇔ 3 x 2 - 2 . 3 x ≥ 0 ⇔ 3 x ≥ 2 ⇔ x ≥ log 3 2 ⇒ 3 sai.
(4) Đường thẳng f(x) = 0 chỉ có 1 nghiệm duy nhất ⇒ 4 sai

Đáp án B
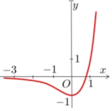
Ta có f x = f x v ớ i x ≥ 0 − f x v ớ i x < 0
Đồ thị hàm số y = f x được suy ra từ đồ thị hàm số y = f x gồm 2 phần:
- Phần 1: Phần phía bên trên trục hoành.
- Phần 2: Lấy đối xứng với phần phía dưới trục Ox qua trục Ox (bỏ đi phần phía dưới trục hoành).
Khi đó ta được đồ thị hàm số y = f x như sau:
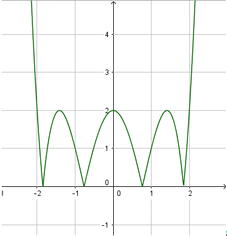
Phương trình f x = log 3 m có 8 nghiệm phân biệt ⇔ 0 < log 3 m < 2 ⇔ 1 < m < 9

Chọn đáp án B
Ta có
![]()
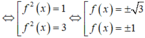
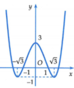
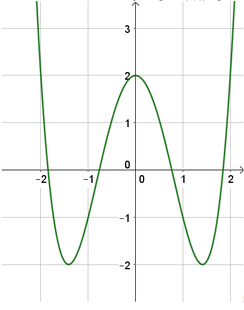
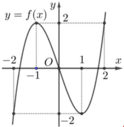
Quan sát đồ thị của hàm số y = f(x) ta thấy:
Phương trình f x = - 3 không có nghiệm; phương trình f x = - 1 có 2 nghiệm;
phương trình f x = 1 có 4 nghiệm; phương trình f x = 3 có 4 nghiệm.
Vậy phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có 10 nghiệm.

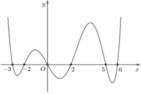
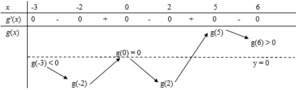
Dựa vào đồ thị hàm số ta thấy

Xét phương trình
![]()
Phương trình (1) có 3 nghiệm phân biệt.
Xét phương trình
![]()
Phương trình (2) có 3 nghiệm phân biệt.
Xét phương trình
![]()
Phương trình (3) có 1 nghiệm duy nhất.
Dễ thấy các nghiệm trên đều không trùng nhau.
Vậy phương trình f f x - 1 = 0 có tất cả 7 nghiệm thực phân biệt.
Chọn C.

Đáp án D
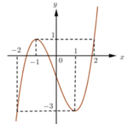
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
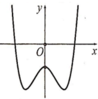






Chọn đáp án A
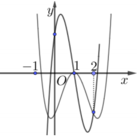
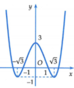
Dựa vào hình dáng cùa đồ thị hàm số y = a x 4 + b x 2 + c ta thấy đây là đồ thị của hàm số bậc bốn trùng phương có 3 điểm cực trị nên phương trình y’=0 có ba nghiệm thực phân biệt.