
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi độ dài hình chiếu thứ nhất là x
=>Độ dài hình chiếu thứ 2 là x+14
Theo đề, ta có: x^2+14x=24^2=576
=>x^2+14x-576=0
=>x=18
=>Độ dai cạnh huyền là 18+18+14=50cm
\(a=\sqrt{18\cdot50}=30\left(cm\right)\)
\(b=\sqrt{32\cdot50}=40\left(cm\right)\)
S=1/2*30*40=15*40=600cm2

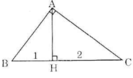
ΔABC vuông tại A và đường cao AH như trên hình.
BC = BH + HC = 1 + 2 = 3
Theo định lí 1:
A B 2 = B H . B C = 1 . 3 = 3
=> AB = √3
Theo định lí 1:
A C 2 = H C . B C = 2 . 3 = 6
=> AC = √6
Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.

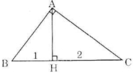
ΔABC vuông tại A và đường cao AH như trên hình.
BC = BH + HC = 1 + 2 = 3
Theo định lí 1: AB2 = BH.BC = 1.3 = 3
=> AB = √3
Theo định lí 1: AC2 = HC.BC = 2.3 = 6
=> AC = √6
Vậy độ dài các cạnh góc vuông của tam giác lần lượt là √3 và √6.

Bài 1:
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)

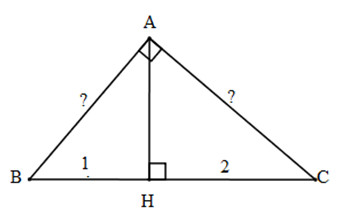
Giả sử tam giác ABC có góc BAC = 90o, AH ⊥ BC, BH = 3, CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
AB2 = BH.BC = 3.(3 + 4) = 3.7 = 21 ⇒ AB = \(\sqrt{21}\)
AC2 = CH.BC = 4.(3 + 4) = 4.7 = 28 ⇒ AC = \(\sqrt{28} = 2\sqrt{7} \)

Gọi độ dài đoạn thẳng ngắn hơn được chia trên cạnh huyền là x (cm) với x>0
\(\Rightarrow\) Độ dài đoạn còn lại là \(x+14\)
Áp dụng hệ thức lượng trong tam giác vuông:
\(24^2=x\left(x+14\right)\)
\(\Leftrightarrow x^2+14x-576=0\Rightarrow\left[{}\begin{matrix}x=18\\x=-32\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\) Độ dài cạnh huyền là: \(18+\left(18+14\right)=50\left(cm\right)\)
Diện tích tam giác: \(S=\dfrac{1}{2}.24.50=600\left(cm^2\right)\)

Giả sử tam giác ABC có góc BAC = 90 ° , AH ⊥ BC, BH = 3, CH = 4
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
A B 2 = BH.BC = 3.(3 + 4) = 3.7 = 21 ⇒ AB = 21
A C 2 = CH.BC = 4.(3 + 4) = 4.7 = 28 ⇒ AC = 28 = 2 7

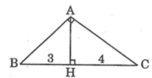
Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH, ta có:
AH2=BH.CH⇒AH=√BH.CH=√1.2=√2
Áp dụng định lí Pytago vào tam giác ABH vuông tại H, ta có:
AH=√BH2+AH2=√1+2=√3AH=BH2+AH2=1+2=3
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
AC=√BC2−AB2=√32−3=√6AC=BC2−AB2=32−3=6



Áp dụng hệ thức lượng trong tam giác ABC vuông tại A có đường cao AH, ta có:
\(AH^2=BH.CH\Rightarrow AH=\sqrt{BH.CH}=\sqrt{4.6}=\sqrt{6}\)
Áp dụng định lí Pytago vào tam giác ABH vuông tại H, ta có:
\(AH=\sqrt{BH^2+AH^2}=\sqrt{4+6}=\sqrt{10}\)
Áp dụng định lí Pytago vào tam giác ABC vuông tại A, ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{10^2-10}=\sqrt{20}\)