Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn làm bài:
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1cm
Tâm O của đường tròn nội tiếp ∆ABC là giao điểm của đường thẳng (d) với cung chứa góc 90° + 60° : 2 = 120° dựng trên đoạn BC cố định
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A. Tam giác ABC là tam giác phải dựng
Dựng BC = 4cm và đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
Tâm O của đường tròn nội tiếp tam giác ABC là giao điểm của đường thẳng (d) với cung chứa góc 90o + 60o : 2 = 120o dựng trên đoạn BC cố định.
Qua B và C vẽ các tiếp tuyến với (O), chúng cắt nhau tại A.
Tam giác ABC là tam giác cần dựng.

Phân tích:
Giả sử dựng được ΔABC thỏa mãn điều kiện.
Gọi O là tâm đường tròn nội tiếp tam giác.
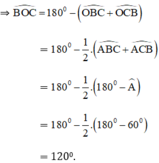
⇒ O thuộc cung m chứa góc 120º dựng trên đoạn BC.
+ Bán kính đường tròn nội tiếp ΔABC bằng 1
⇒ O cách BC 1cm
⇒ O thuộc d // BC và cách BC 1cm.
Vậy O là giao của cung m và đường thẳng d.
+ Khi đó ta dựng được đường tròn (O; 1) nội tiếp ΔABC
⇒ A là giao của tiếp tuyến đi qua B và C của đường tròn (O; 1).
Cách dựng:
+ Dựng BC = 4cm
+ Dựng đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
+ Dựng cung m chứa góc 120º trên đoạn BC.
+ (d) cắt cung m tại O.
+ Dựng đường tròn tâm O, bán kính 1cm.
+ Kẻ tiếp tuyến từ B và C đến (O; 1cm).
Hai tiếp tuyến cắt nhau tại A.
ΔABC là tam giác cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 4cm .
+ O thuộc cung 120º dựng trên đoạn BC
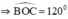
+ A là giao của 2 tiếp tuyến
⇒ (O; 1cm) tiếp xúc với AB và AC
Mà khoảng cách từ O đến BC = 1cm
⇒ (O; 1cm) cũng tiếp xúc với BC
⇒ (O; 1cm) là đường tròn nội tiếp ΔABC
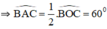
Vậy ΔABC có BC = 4cm,  , đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
, đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
Biện luận:
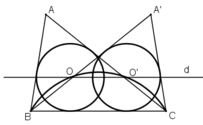
Vì d cắt m tại hai điểm nên bài toán có hai nghiệm hình ΔABC và ΔA’BC như hình vẽ.

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
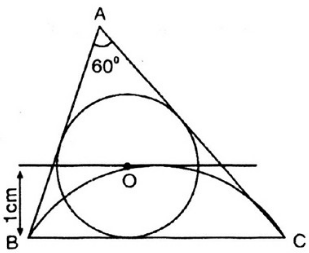
Phân tích:
Giả sử dựng được ΔABC thỏa mãn điều kiện.
Gọi O là tâm đường tròn nội tiếp tam giác.
⇒ O thuộc cung m chứa góc 120 º dựng trên đoạn BC.
+ Bán kính đường tròn nội tiếp ΔABC bằng 1
⇒ O cách BC 1cm
⇒ O thuộc d // BC và cách BC 1cm.
Vậy O là giao của cung m và đường thẳng d.
+ Khi đó ta dựng được đường tròn (O; 1) nội tiếp ΔABC
⇒ A là giao của tiếp tuyến đi qua B và C của đường tròn (O; 1).
Cách dựng:
+ Dựng BC = 4cm
+ Dựng đường thẳng (d) song song với BC và cách BC một khoảng là 1 cm.
+ Dựng cung m chứa góc 120 º trên đoạn BC.
+ (d) cắt cung m tại O.
+ Dựng đường tròn tâm O, bán kính 1cm.
+ Kẻ tiếp tuyến từ B và C đến (O; 1cm).
Hai tiếp tuyến cắt nhau tại A.
ΔABC là tam giác cần dựng.
Chứng minh:
+ Theo cách dựng có BC = 4cm .
+ O thuộc cung 120º dựng trên đoạn BC
+ A là giao của 2 tiếp tuyến
⇒ (O; 1cm) tiếp xúc với AB và AC
Mà khoảng cách từ O đến BC = 1cm
⇒ (O; 1cm) cũng tiếp xúc với BC
⇒ (O; 1cm) là đường tròn nội tiếp ΔABC
Vậy ΔABC có BC = 4cm, , đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
, đường tròn nội tiếp có bán kính 1cm thỏa mãn yêu cầu.
Biện luận:
Vì d cắt m tại hai điểm nên bài toán có hai nghiệm hình ΔABC và ΔA’BC như hình vẽ.