PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
SG
1
SG
1
8 tháng 6 2017
Lấy đối xứng qua đường thẳng AB, ta được cung chứa góc thứ hai thỏa mãn bài toán.
Chú ý : Cung nhỏ AB trong cách dựng trên là cung chứa góc \(120^0\)
2 tháng 6 2017
Chọn phương án (D) :
Quỹ tích các điểm M nhìn đoạn thẳng AB dưới 1 góc \(120^0\) là hai cung chứa góc \(120^0\) (đối xứng nhau) dựng trên hai điểm A, B.
22 tháng 1 2021
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc = 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
VT
23 tháng 2 2021
Dựng đoạn thẩng AB bằng 3cm dựng góc xAB =55* dựng tia AY vuông góc vs tia Ax dựng đg trung trực d của đoạn thẳng AB/ d cắt Ay tại O . Dựng đg tròn tâm O bán kính OA cung AmB là góc 55 độ cần dựng
PT
1
CM
26 tháng 5 2017
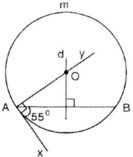
Cách dựng:
+ Dựng đoạn thẳng AB = 3cm.
+ Dựng góc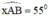 
+ Dựng tia Ay vuông góc với tia Ax.
+ Dựng đường trung trực d của đoạn thẳng AB.
+ d cắt Ay tại O.
+ Dựng đường tròn tâm O, bán kính OA.
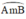là cung chứa góc
55
º
cần dựng.
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒ 
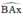là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M ∈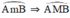 
là góc nội tiếp chắn cung nhỏ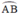 
⇒ 
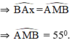
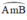là cung chứa góc
55
º
dựng trên đoạn AB = 3cm.
Kết luận: Bài toán có một nghiệm hình.
11 tháng 4 2017
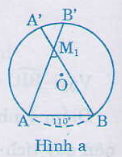
M1 là điểm bất kì nằm trong cung chứa góc 550 (hình a).
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương) Vậy góc AM1B > 550
b)
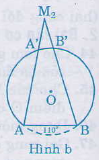
M2 là điểm bất kì nằm ngoài đường tròn (h.b), M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550
LH
11 tháng 4 2017
M1 là điểm bất kì nằm trong cung chứa góc 550 .
Gọi B’, A’ theo thứ tự là giao điểm của M1A, M1B với cung tròn. Vì góc AM1B là góc có đỉnh nằm trong đường tròn, nên: góc AM1B = sđ cung(AB +A’B’)/2 = sđcung AB/2 + sđcung A’B’/2 = 550+ (một số dương)
Vậy góc AM1B > 550
b)
M2 là điểm bất kì nằm ngoài đường tròn , M2A, M2B lần lượt cắt đường tròn tại A’, B’. Vì góc AM2B là góc có đỉnh nằm bên ngoài đường tròn nên: góc AM2B= sđcung(AB – A’B’)/2= sđAB/2 – sđA’B’/2 = 550 – (một số dương)
Vậy góc AM2B < 550
SG
2
11 tháng 4 2017
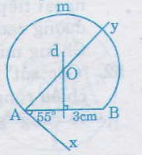
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc = 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: 
là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
LH
11 tháng 4 2017
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc \(\widehat{xAB}\)= 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
Cách dựng:
+ Dựng đoạn thẳng AB = 3cm.
+ Dựng góc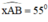
+ Dựng tia Ay vuông góc với tia Ax.
+ Dựng đường trung trực d của đoạn thẳng AB.
+ d cắt Ay tại O.
+ Dựng đường tròn tâm O, bán kính OA.
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒
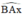là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M ∈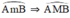
là góc nội tiếp chắn cung nhỏ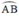 
⇒
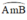là cung chứa góc 55º dựng trên đoạn AB = 3cm.
Kết luận: Bài toán có một nghiệm hình.