Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

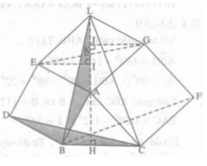
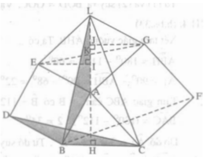
+) Xét tam giác EIA vuông tại I nên :
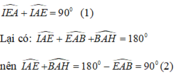
+) Xét hai tam giác ABH và ∆EAI có:
AB = AE ( vì ABDE là hình vuông)
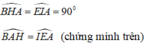
Suy ra: ∆ABH = ∆ EAI ( cạnh huyền – góc nhọn)
⇒ AH = EI ( hai cạnh tương ứng)
+) Tương tự hai tam giác vuông ACH và GAJ bằng nhau.
⇒ AH = GJ.
Suy ra EI = AH = GJ.
+) Xét ΔEKI và ΔGKJ có:
EI = GJ ( chứng minh trên)
∠(IKE) = ∠(JKG) (đối đỉnh).
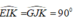
do đó ΔEKI = ΔGKJ ( cgv – gn)
suy ra: KE = KG
Từ đó ta có K trung điểm của EG. Vậy AK là trung tuyến của tam giác AEG.

A B C H K D I
Xét tam giác ABH và tam giác KHC ta có
AH=HK (gt)
BH=HC ( H là trung điểm BC)
góc AHB=góc KHC (=90)
-> tam giác ABH= tam giác KHC (c-g-c)
b)
Xét tam giác ABH và tam giác AHC ta có
AH=AH (cạnh chung)
BH=HC ( H là trung điểm BC)
AB=AC (ggt)
-> tam giác ABH= tam giác AHC (c-c-c)
-> góc AHB= góc AHC (2 góc tương ứng)
mà góc AHB + góc AHC =180 ( 2 góc kề bù)
nên góc AHB + góc ABH=180
->2 góc AHB=180
-> góc AHB =180 :2 =90
=> AH vuông góc BC tại H
c) Xét tam giác BDH và tam giác HAB ta có
BH=BH ( cạnh chung)
góc DBH= góc BHA (=90)
góc DHB= goc1HBA ( 2 góc sole trong và AB//DH)
-> tam giác BDH=tam giác HAB ( g-c-g)
-> DH=AB ( 2 cạnh tương ứng)
d) ta có DH=AB (cmt)
KC=AB ( tam giác AHB= tam giác KHC)
-> DH = KC
ta có góc BAH = góc HKC ( tam giác AHB= tam giác KHC)
mà 2 góc nằm ở vị trí sole trong
nên AB//CK
mặt khác AB//DH (gt)
do đó CK//DH
Xét tam giác DHI và tam giác CKI ta có
HI=IK (I là trung điểm HK)
DH=Ck (cmt)
góc IHD=góc IKC (2 góc sole trong và DH//CK)
-> tam giác DHI= tam giác CKI (c-g-c)
-> góc DHI = góc CIK (2 góc tương ứng
mà góc CIK + góc HIC =180 ( 2 góc kề bù)
nên góc DHI+ góc HIC =180
-> góc DIC =180
-> D,I,C thẳng hàng

Theo a) ΔEKI = ΔGKJ nên KI = KJ.
Mặt khác, theo giả thiết K là trung điểm của AL nên KA = KL.
Suy ra: KA – KI = KL – KJ hay IA= JL.
Ta có: ∆ACH= ∆ GAJ ( theo a) nên HC = AJ;
∆ABH = ∆ EAI nên BH = AI.
+) Suy ra:
AL = AJ + JL = AJ + AI = HC + HB = BC

a, BE=CD và BE vuông góc với CD.
b, KL là trung điểm cuarDE và AK=1/2BC.

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A