Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Áp suất: \(p = \frac{F}{S}\)
+ F: đơn vị N
+ S: đơn vị \({m^2}\)
=> Đơn vị p là \(N/{m^2} = Pa\)
- Khối lượng riêng: \(\rho = \frac{m}{V}\)
+ m: đơn vị kg
+ V: đơn vị \({m^3}\)
=> Đơn vị của \(\rho \) là \(kg/{m^3}\)

- Áp suất: \(p=\dfrac{F}{S}\)
+ \(F\): đơn vị \(N\)
+ \(S\): đơn vị \(m^2\)
\(\Rightarrow\) Đơn vị \(p\) là \(N/m^2=Pa\)
- Khối lượng riêng: \(\rho=\dfrac{m}{V}\)
+ \(m\): đơn vị \(kg\)
+ \(V\): đơn vị \(m^3\)
\(\Rightarrow\) Đơn vị của \(\rho\) là \(kg/m^3\)

Số đo độ biến thiên nội năng trong quá trình truyền nhiệt là nhiệt lượng: Q = ΔU
(đơn vị của Q và ΔU là Jun)
Công thức tính nhiệt lượng vật thu vào hay tỏa ra khi nhiệt độ của vật thay đổi:
Q = m.c.Δt; Trong đó c là nhiệt dung riêng (J/kg.K), Δt là độ tăng hoặc giảm của nhiệt độ (ºC hoặc K), m là khối lượng của vật (kg).

Bài làm.
Nguyên lí thứ nhất của NĐLH là sự vận dụng định luật bản loàn và chuyển hoá năng lượng vào các hiện tượng nhiệt. Sau đây là một trong nhiều cách phát biểu nguyên lí này.
Độ biên thiên nội năng của hệ bằng tổng công và nhiệt lượng mà hệ nhận được.
ΔU = A + Q
Với quy ước về dấu thích hợp, biểu thức trên có thể dùng để diễn đạt các quá trình truyền và chuyển hoá năng lượng khác như vật truyền nhiệt, vật thực hiện công, vật thu nhiệt và thực hiện công...
Có những cách quy ước về dấu của nhiệt lượng và công khác nhau. Sau đây là quy ước dùng trong sách này
Q > 0: Hệ nhận nhiệt lượng;
Q < 0: Hệ truyền nhiệt lượng;
A > 0: Hệ nhận công;
A < 0: Hệ thực hiện công.

Nguyên lí I nhiệt động lực học: Độ biến thiên nội năng của vật bằng tổng công và nhiệt lượng mà vật nhận được: δU = A + Q
Qui ước dấu:
+ Q > 0 vật nhận nhiệt lượng
+ Q < 0 vật truyền nhiệt lượng
+ A > 0 vật nhận công
+ A < 0 vật thực hiện công

Ta có thứ nguyên của khối lượng m là M, thứ nguyên của thể tích V là L3
=> Thứ nguyên của khối lượng riêng ρ là M.L-3
=> Đơn vị của ρ trong hệ SI là kg/m3
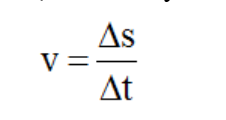
Biểu thức (4): \(v = \omega .r\)
Ta biểu diễn biểu thức (4) sang đơn vị, ta có:
\(\left[ {\frac{m}{s}} \right] = \left[ {\frac{1}{s}} \right].\left[ m \right]\)
=> Biểu thức (4) đúng