Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) (3x2 - 7x – 10)[2x2 + (1 - √5)x + √5 – 3] = 0
=> hoặc (3x2 - 7x – 10) = 0 (1)
hoặc 2x2 + (1 - √5)x + √5 – 3 = 0 (2)
Giải (1): phương trình a - b + c = 3 + 7 - 10 = 0
nên
x1 = - 1, x2 = =
Giải (2): phương trình có a + b + c = 2 + (1 - √5) + √5 - 3 = 0
nên
x3 = 1, x4 =
b) x3 + 3x2– 2x – 6 = 0 ⇔ x2(x + 3) – 2(x + 3) = 0 ⇔ (x + 3)(x2 - 2) = 0
=> hoặc x + 3 = 0
hoặc x2 - 2 = 0
Giải ra x1 = -3, x2 = -√2, x3 = √2
c) (x2 - 1)(0,6x + 1) = 0,6x2 + x ⇔ (0,6x + 1)(x2 – x – 1) = 0
=> hoặc 0,6x + 1 = 0 (1)
hoặc x2 – x – 1 = 0 (2)
(1) ⇔ 0,6x + 1 = 0
⇔ x2 = =
(2): ∆ = (-1)2 – 4 . 1 . (-1) = 1 + 4 = 5, √∆ = √5
x3 = , x4 =
Vậy phương trình có ba nghiệm:
x1 = , x2 =
, x3 =
,
d) (x2 + 2x – 5)2 = ( x2 – x + 5)2 ⇔ (x2 + 2x – 5)2 - ( x2 – x + 5)2 = 0
⇔ (x2 + 2x – 5 + x2 – x + 5)( x2 + 2x – 5 - x2 + x - 5) = 0
⇔ (2x2 + x)(3x – 10) = 0
⇔ x(2x + 1)(3x – 10) = 0
Hoặc x = 0, x = , x =
Vậy phương trình có 3 nghiệm:
x1 = 0, x2 = , x3 =
a) \(3x^3+6x^2-4x=0\) \(\Leftrightarrow\) \(x\left(3x^2+6x-4\right)=0\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=0\\3x^2+6x-4=0\end{matrix}\right.\) \(\Leftrightarrow\) \(\left\{{}\begin{matrix}x=0\\\left\{{}\begin{matrix}x=\dfrac{-3+\sqrt{21}}{3}\\x=\dfrac{-3-\sqrt{21}}{3}\end{matrix}\right.\end{matrix}\right.\)
vậy phương trình có 2 nghiệm \(x=0;x=\dfrac{-3+\sqrt{21}}{3};x=\dfrac{-3-\sqrt{21}}{3}\)
Bài 3: \(3\left(\sqrt{2x^2+1}-1\right)=x\left(1+3x+8\sqrt{2x^2+1}\right)\)
\(\Leftrightarrow\left(3-8x\right)\sqrt{2x^2+1}=3x^2+x+3\)
\(\Rightarrow\left(3-8x\right)^2\left(2x^2+1\right)=\left(3x^2+x+3\right)^2\)
\(\Leftrightarrow119x^4-102x^3+63x^2-54x=0\)
\(\Leftrightarrow x\left(7x-6\right)\left(17x^2+9\right)=0\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{6}{7}\end{cases}}\)
Thử lại, ta nhận được \(x=0\)là nghiệm duy nhất của phương trình
a,x4-10x2+9=0
=>(x-1)(x3+x2-9x-9)=0
=> (x-1)(x+1)(x-3)(x+3)=0
=>\(\orbr{\begin{cases}x-1=0\\x+1=0\end{cases}}\)hoặc\(\orbr{\begin{cases}x-3=0\\x+3=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=\pm1\\x=\pm3\end{cases}}\)
Vậy tập nghiệm cuả pt là S={\(\pm1,\pm3\)}
Bài giải:
a) 3x2 – 2x = x2 + 3 ⇔ 2x2 – 2x - 3 = 0.
b’ = -1, ∆’ = (-1)2 – 2 . (-3) = 7
x1 =
≈ 1, 82; x2 = 
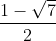≈ -0,82
b) (2x - √2)2 – 1 = (x + 1)(x – 1) ⇔ 3x2 - 4√2 . x + 2 = 0 . b’ = -2√2
∆’ = (-2√2)2 – 3 . 2 = 2
x1 =
= √2 ≈ 1,41; x2 =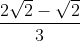 
= 
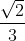≈ 0,47.
c) 3x2 + 3 = 2(x + 1) ⇔ 3x2 – 2x + 1 = 0.
b’ = -1; ∆’ = (-1)2 – 3 . 1 = -2 < 0
Phương trình vô nghiệm.
d) 0,5x(x + 1) = (x – 1)2 ⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0, b’ = -2,5; ∆’ = (-2,5)2 – 1 . 2 = 4,25
x1 = 2,5 + √4,25 ≈ 4,56, x2 = 2,5 - √4,25 ≈ 0,44
(Rõ ràng trong trường hợp này dung công thức nghiệm thu gọn cũng không đơn giản hơn)
a) 3x2 – 2x = x2 + 3 ⇔ 2x2 – 2x - 3 = 0.
b’ = -1, ∆’ = (-1)2 – 2 . (-3) = 7
x1 =
≈ 1, 82; x2 = 
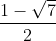≈ -0,82
b) (2x - √2)2 – 1 = (x + 1)(x – 1) ⇔ 3x2 - 4√2 . x + 2 = 0 . b’ = -2√2
∆’ = (-2√2)2 – 3 . 2 = 2
x1 =
= √2 ≈ 1,41; x2 =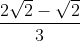 
= 
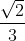≈ 0,47.
c) 3x2 + 3 = 2(x + 1) ⇔ 3x2 – 2x + 1 = 0.
b’ = -1; ∆’ = (-1)2 – 3 . 1 = -2 < 0
Phương trình vô nghiệm.
d) 0,5x(x + 1) = (x – 1)2 ⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0, b’ = -2,5; ∆’ = (-2,5)2 – 1 . 2 = 4,25
x1 = 2,5 + √4,25 ≈ 4,56, x2 = 2,5 - √4,25 ≈ 0,44