Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(3+2\sqrt{2}=2+2\sqrt{2}+1=\left(\sqrt{2}^2\right)+2\times\sqrt{2}\times1=\left(\sqrt{2}+1\right)^2\)
mấy câu còn lại tương tự

a) \(9+4\sqrt{5}=\left(\sqrt{5}\right)^2+2.\sqrt{5}.2+2^2=\left(\sqrt{5}+2\right)^2\)
b) \(23-8\sqrt{7}=4^2-2.4.\sqrt{7}+\left(\sqrt{7}\right)^2=\left(4-\sqrt{7}\right)^2\)
c) \(4-2\sqrt{3}=\left(\sqrt{3}\right)^2-2.\sqrt{3}.1+1^2=\left(\sqrt{3}-1\right)^2\)
d) \(11+6\sqrt{2}=3^2+2.3.\sqrt{2}+\left(\sqrt{2}\right)^2=\left(3+\sqrt{2}\right)^2\)
a) \(9+4\sqrt{5}=\left(\sqrt{5}+2\right)^2\)
b) \(23-8\sqrt{7}=\left(4-\sqrt{7}\right)^2\)
c) \(4-2\sqrt{3}=\left(\sqrt{3}-1\right)^2\)
d) \(11+6\sqrt{2}=\left(3+\sqrt{2}\right)^2\)

Ta chỉ cần đưa \(4\sqrt{3}=2.\sqrt{a}.\sqrt{b}\) sao cho a+b=7 hoặc a+b=13
a) \(7+4\sqrt{3}=7+2\sqrt{4}.\sqrt{3}=\left(\sqrt{4}\right)^2+2\sqrt{4}.\sqrt{3}+\left(\sqrt{3}\right)^2=\left(\sqrt{4}+\sqrt{3}\right)^2\)
b) \(13-4\sqrt{3}=\left(\sqrt{12}\right)^2-2.\sqrt{12}.1+1^2=\left(\sqrt{12}-1\right)^2\)
Cái này mk hk rồi nè
\(7+4\sqrt{3}=4+2.2.\sqrt{3}+3=\left(\sqrt{3}+2\right)^2\)
\(13-4\sqrt{3}=12-2.2.\sqrt{3}+1=12-2.\sqrt{12}+1=\left(\sqrt{12}-1\right)^2\)
k mk nha

a/ 3 + 2\(\sqrt{2}\) = 2 + 2\(\sqrt{2}\) + 1 = \(\sqrt{2}^2\) + 2\(\sqrt{2}\) + 12 = ( \(\sqrt{2}\) + 1 )2
b/ 3 - \(\sqrt{8}\) = 2 - \(\sqrt{4.2}\) + 1 = 2 - 2\(\sqrt{2}\) + 1 = \(\sqrt{2}^2\) - 2\(\sqrt{2}\) + 12
= ( \(\sqrt{2}\) - 1 )2
c/ 9 + 4\(\sqrt{5}\) = 4 + 2.2\(\sqrt{5}\) + 5 = 22 + 2.2\(\sqrt{5}\) + \(\sqrt{5}\)2
= ( 2 + \(\sqrt{5}\) )2
d/ 23 - 8\(\sqrt{7}\) = 16 - 2.4.\(\sqrt{7}\) + 7 = 42 - 2.4.\(\sqrt{7}\) + \(\sqrt{7}^2\)
= ( 4 - \(\sqrt{7}\) )2

\(13-4\sqrt{3}=\left(2\sqrt{3}\right)^2-2.2\sqrt{2}.1+1^2=\left(2\sqrt{3}-1\right)^2\)
a) \(\left(\sqrt{5}+\sqrt{3}\right)\sqrt{8-2\sqrt{15}}=\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)=5-3=2\)
câu này \(\sqrt{15}\)đúng hơn \(\sqrt{5}\)
b) \(\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}=\frac{\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}}{\sqrt{2}}=\frac{\sqrt{5}-1-\sqrt{5}-1}{\sqrt{2}}=\frac{-2}{\sqrt{2}}=-\sqrt{2}\)c) \(\sqrt{5-2\sqrt{6}}-\sqrt{5+2\sqrt{6}}=\sqrt{3}-\sqrt{2}-\sqrt{3}-\sqrt{2}=-2\sqrt{2}\)

Bài 1:
a: Ta có: \(\sqrt{3x^2}=\sqrt{12}\)
\(\Leftrightarrow3x^2=12\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
b: Ta có: \(\sqrt{\left(x-2\right)^2}=3\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3\\x-2=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\end{matrix}\right.\)

\(12-2\sqrt{35}\)
\(=\left(\sqrt{5}\right)^2+\left(\sqrt{7}\right)^2-2\sqrt{35}\)
\(=\left(\sqrt{5}+\sqrt{7}\right)^2\)
\(7+\sqrt{40}\)
\(=\left(\sqrt{5}\right)^2+\left(\sqrt{2}\right)^2+2\sqrt{10}\)
\(=\left(\sqrt{5}+\sqrt{2}\right)^2\)
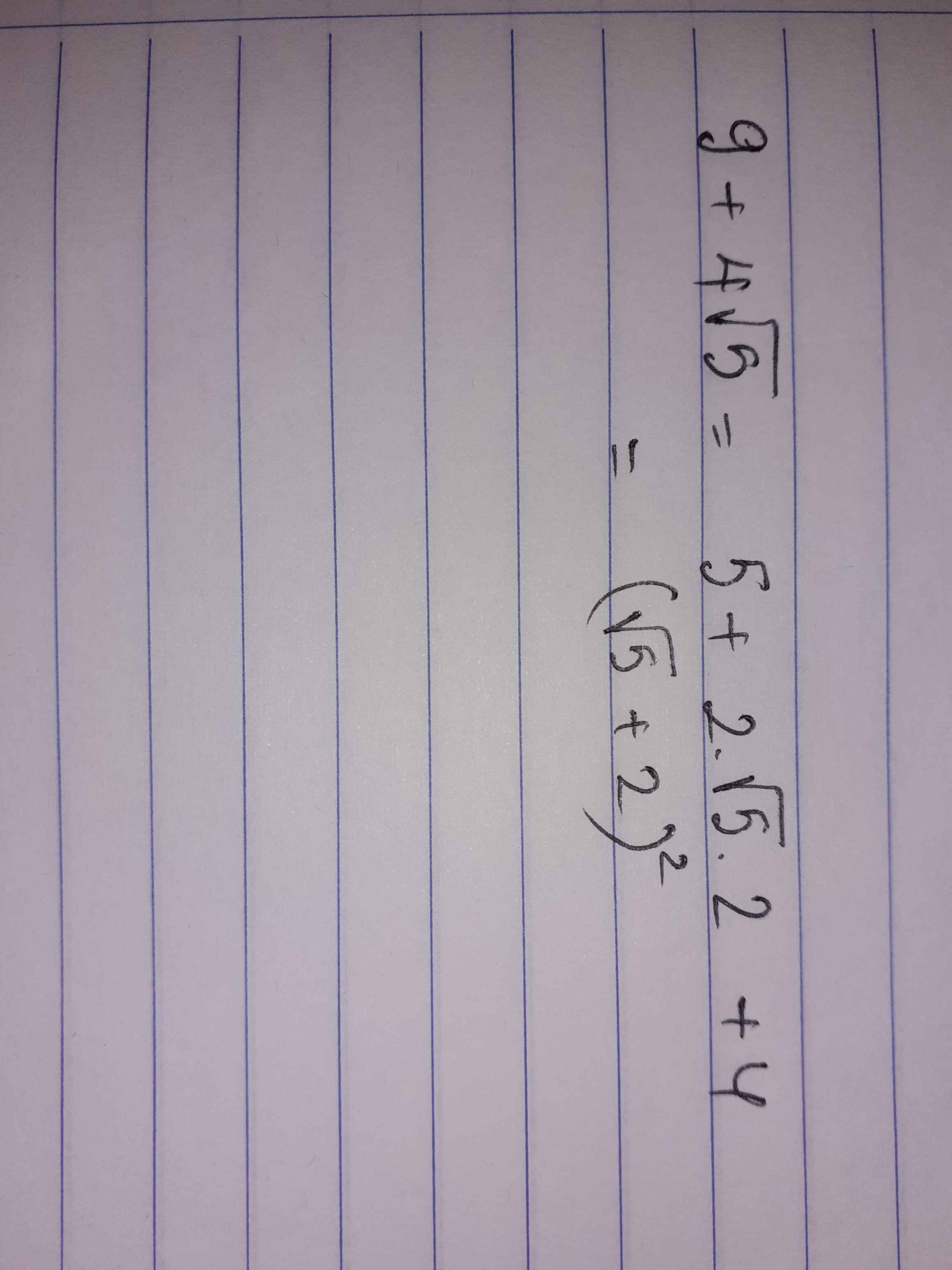
\(3-\sqrt{8}=3-2\sqrt{2}=\left(\sqrt{2}\right)^2-2.\sqrt{2}.1+1^2=\left(\sqrt{2}-1\right)^2\)
3 - \(\sqrt{8}\)
= 3 - 2\(\sqrt{2}\)
= 1 - 2\(\sqrt{2}\) + 2
= \(\left(1-\sqrt{2}\right)^2\)