Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số hạt nhân Natri là \(N_0 = nN_Á = \frac{m}{A}N_A\)
Độ phóng xạ ban đầu \(H_0 = \lambda N_0 = \frac{\ln 2}{T}\frac{m}{A}N_A= 6,73.10^{16}.(Bq)\)
Chú ý là trong khi tính độ phóng xạ theo đơn vị "Bq" thì chu kì phải đổi sang đơn vị "giây" .

Khối lượng chất phóng xạ đã bị phân rã là
\(\Delta m = m_0(1-2^{-\frac{t}{T}}) \)
=> \(\frac{\Delta m }{m_0}= 0,75 =1- 2^{-\frac{t}{T}}\)
=> \(t = -T\ln_20,25 = 30h.\)

Kí hiệu \(N_{01}\), \(N_{02}\) là số hạt ban đầu lần lượt của \(^{235}U\) và \(^{238}U\).
t = 0 Ban đầu t thời điểm cần xác định hiện nay t 1 2
Hiện nay \(t_2\): \(\frac{N_{1}}{N_{2}}=\frac{N_{01}2^{-\frac{t_2}{T_1}}}{N_{02}2^{-\frac{t_2}{T_2}}} =\frac{7}{1000}.(1)\)
Thời điểm \(t_1\):
\(\frac{N_1}{N_2}= \frac{N_{01}2^{-\frac{t_1}{T_1}}}{N_{02}2^{-\frac{t_1}{T_2}}} = \frac{3}{100}.(2)\)
Chia (1) cho (2) => \(\frac{2^{-\frac{t_2}{T_1}}.2^{-\frac{t_1}{T_2}}}{2^{-\frac{t_1}{T_1}}.2^{-\frac{t_2}{T_2}}}= \frac{7.100}{3.1000}= \frac{7}{30}.\)
Áp dụng \(\frac{1}{2^{-x}} =2^x. \)
=> \(2^{(t_2-t_1)(\frac{1}{T_2}-\frac{1}{T_1})} = \frac{7}{30}.\)
=> \(t_2-t_1 = \frac{T_1T_2}{T_1-T_2}\ln_2 (7/30)=1,74.10^{9}\).(năm) \(= 1,74 \)(tỉ năm).
Như vậy cách hiện nay 1,74 tỉ năm thì trong urani tự nhiên có tỉ lệ số hạt thỏa mãn như bài cho.

Số hạt nhân Pôlôni lúc đầu là \(N_ 0 = nN_A= \frac{m_0}{A}N_A= \frac{42.10^{-3}.6,02.10^{23}}{210}= 1,204.10^{20}\)
Độ phóng xạ ban đầu là \(H_0 = \lambda N_0 = \frac{\ln 2}{T}N_0 = \frac{\ln 2}{140.24.3600}1,204.10^{20}= 6,9.10^{12}.(Bq)\)
Chú ý: Khi tính độ phóng xạ theo đơn vị Bq thì thời gian chu kì phải chuyển sang "giây"

Số hạt nhân chưa phóng xạ chính là số hạt nhân còn lại
\(N= N_0 2^{-\frac{t}{T}}= N_0 .2^{-4}= \frac{1}{16}N_0.\)

Đáp án: D.
Phương trình phóng xạ: ![]()
Vì số khối của Na và Mg bằng nhau nên sau mỗi phản ứng khối lượng Mg24 được tạo thành đúng bằng khối lượng Na24 bị phân rã.
Gọi m0 là khối lượng ban đầu của Na24. Khối lượng Mg24 lúc đầu: m1 = m0/4
Sau t = 2T: Khối lượng Na24 còn lại là: m = m0/22 = m0/4
Khối lượng Mg24 được tạo thành: m2 = ∆ m = m0 – m = 3m0/4
Lúc đó khối lượng Mg24 trong hỗn hợp là: m’ = m1 + m2 = m0
Do đó tỉ số m’/m = 4.

- Phương trình phóng xạ:
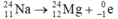
- Vì số khối của Na và Mg bằng nhau nên sau mỗi phản ứng khối lượng Mg24 được tạo thành đúng bằng khối lượng Na24 bị phân rã.
- Gọi m0 là khối lượng ban đầu của Na24. Khối lượng Mg24 lúc đầu: m1 = m0/4
- Sau t = 2T: Khối lượng Na24 còn lại là: m = m0/22 = m0/4
- Khối lượng Mg24 được tạo thành: m2 = Δm = m0 – m = 3m0/4
- Lúc đó khối lượng Mg24 trong hỗn hợp là: m’ = m1 + m2 = m0
→ Do đó tỉ số: m’/m = 4.

Do hạt nhân mẹ Po ban đầu đứng yên, áp dụng định luật bảo toàn động lượng trước và sau phản ứng ta thu được
\(P_{\alpha} = P_{Pb} \)
=> \(2m_{\alpha} K_{\alpha}=2m_{Pb}K_{Pb} \)
=> \( 4,0026.K_{\alpha}=205,9744.K_{Rn}.(1)\)
Áp dụng định luật bảo toàn năng lượng toàn phần có
\(K_{\alpha}+K_{Pb} = (m_t-m_s)c^2\)
=> \(K_{\alpha}+K_{Rn} = (m_{Po}-m_{\alpha}-m_{Pb})c^2= 0,0058.931,5 = 5,4027 MeV. (2)\)
Từ (1) và (2) giải hệ phương trình ta được
\(K_{\alpha} = 5,2997 MeV; K_{Pb} = 0,103 MeV. \)
=> \(v_{Pb}= \sqrt{\frac{2K_{Pb}}{m_{Pb}}} =\sqrt{\frac{2.0,103.10^6.1,6.10^{-19}}{205,9744.1,66055.10^{-27}}} = 3,06.10^5m/s.\)
Chú ý đổi đơn vị \(1 MeV = 10^6.1,6.10^{-19}J ; 1 u = 1,66055.10^{-27} kg.\)

Số hạt nhân chưa bị phân rã (số hạt nhân còn lại)
\(N= N_0 2^{-\frac{t}{T}} = N_02^{-\frac{0,5T}{T}}= N_02^{-0,5}= \frac{N_0}{\sqrt{2}}.\)
Phương trình phóng xạ: 2411Na → 2412Mg + 0-1e
Vì số khối của Na và Mg bằng nhau nên sau mỗi phản ứng khối lượng Mg24 được tạo thành đúng bằng khối lượng Na24 bị phân rã.
Gọi m0 là khối lượng ban đầu của Na24. Khối lượng Mg24 lúc đầu: m1 = m0/4
Sau t = 2T: Khối lượng Na24 còn lại là: m = m0/22 = m0/4
Khối lượng Mg24 được tạo thành: m2 = Dm = m0 – m = 3m0/4
Lúc đó khối lượng Mg24 trong hỗn hợp là: m’ = m1 + m2 = m0
Do đó tỉ số: m’/m = 4.,
Chọn đáp án D