Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
R thay đổi để PR max thì: \(R=\sqrt{r^2+(Z_L-Z_C)^2}=Z_{NB}\)
\(\Rightarrow U_R=U_{NB}=80\sqrt 3\) (V) (1)
\(U^2=(U_R+U_r)^2+(U_L-U_C)^2=240^2\) (2)
Và: \(U_{NB}^2=U_r^2+(U_L-U_C)^2=3.80^2\) (3)
Lấy (2) - (3) vế với vế ta có: \((U_R+2U_r).U_R=6.80^2\Rightarrow U_r=40\sqrt 3\)
Vậy hệ số công suất: \(\cos\varphi=\dfrac{U_r+U_R}{U}=\dfrac{\sqrt 3}{2}\)

\(Z_{L1}=\omega_1.L=30\) (1)
\(Z_{C1}=\dfrac{1}{\omega_1C}=40\) (2)
Lấy (1) chia (2) vế với vế ta được: \(\omega_1^2LC=\dfrac{3}{4}\) (3)
Khi tần số \(\omega_2\) thì hệ số công suất bằng 1
\(\Rightarrow Z_{L2}=Z_{C2}\Rightarrow \omega_2.L=\dfrac{1}{\omega_2C}\)
\(\Rightarrow \omega_{2}^2LC=1\) (4)
Lấy (4) chia (3) vế với vế \(\Rightarrow \dfrac{\omega_2}{\omega_1}=\dfrac{2}{\sqrt 3}\Rightarrow \omega_2=\dfrac{2}{\sqrt 3}\omega_1\)
Chọn B.

Áp dụng: \(\dfrac{2}{L_0}=\dfrac{1}{L_1}+\dfrac{1}{L_2}\)
Suy ra \(L_0=\dfrac{3}{2\pi}(H)\)

Khi C = C1 hoặc C = C2 thì I như nhau, do vậy:
\(Z_1=Z_2\Rightarrow Z_L-Z_{C1}=Z_{C2}-Z_L\Rightarrow Z_L=\dfrac{Z_{C1}+Z_{C2}}{2}=45\Omega\)
Để cường độ hiệu dụng qua R cực đại thì mạch xảy ra cộng hưởng.
\(\Rightarrow Z_C=Z_L=45\Omega\)
Chọn A.

Đặt điện áp u = U0cos100πt vào hai đầu đoạn mạch AB theo thứ tự gồm R

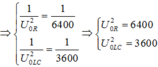
=> Điện áp cực đại:
![]()

Bài này chỉ cần sử dụng công thức 2 giá trị của C để có cùng 1 giá trị của $U_C$ :
$U_C=U_{C_{max}} \cos \left(\dfrac{\varphi _1-\varphi _2}{2} \right)$
$\Rightarrow U_{C_{max}}=\dfrac{60}{\cos \dfrac{\pi }{6}}=40\sqrt{3} V$
Khi $U_{C_{max}}$ ta có:
$P=\dfrac{U^2}{R}\cos ^2\varphi _3=P_{max}\cos ^2\varphi _3=\dfrac{P_{max}}{2}$
$\Rightarrow \cos \varphi _3=\dfrac{\sqrt{2}}{2}$
Vẽ giản đồ suy ra: $U=\dfrac{U_{C_{max}}}{\sqrt{2}}=20\sqrt{6}\left(V \right)$
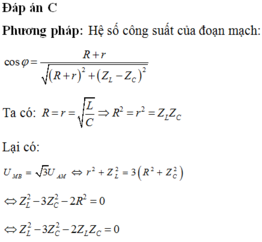

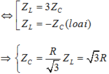
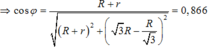


\(Z_C=40\Omega\)
Đoạn mạch AM có: \(\tan\varphi_{AM~i}=\frac{-Z_C}{R_1}=-1\)\(\Rightarrow\varphi_{AM~i}=-\frac{\pi}{4}\)\(\Rightarrow\varphi_{AM}-\varphi_i=-\frac{\pi}{4}\Rightarrow\varphi_i=\varphi_{AM}+\frac{\pi}{4}=-\frac{7\pi}{12}+\frac{\pi}{4}=-\frac{\pi}{3}\)
\(u_{AB}\) là tổng hợp của \(u_{AM}\) và \(u_{MB}\) nên: \(u_{AB}=221\cos\left(100\pi t-0,587\right)\)(Tổng hợp bằng máy tính) \(\Rightarrow\varphi_{AB}=-0,587\)
Như vậy, độ lệch pha của \(u_{AB}\) đối với \(i\)là: \(\varphi=\varphi_{AB}-\varphi_i=-0,587+\frac{\pi}{3}=0,46\)
Hệ số công suất \(\cos\varphi=\cos0,46=0,896\)