Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

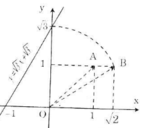
Ta có: \(\sqrt{3}\) = \(\sqrt{2+1}\) = \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)
Hình vẽ SGK có : OC = OB = \(\sqrt{2}\) và theo định lí Py-ta-go t a có :
OD = \(\sqrt{OC^2+CD^2}\)= \(\sqrt{\left(\sqrt{2}\right)^2+1^2}\)= \(\sqrt{3}\)
Dùng compa ta xác định được điểm biểu diễn số \(\sqrt{3}\). trên Oy. Từ đó xác định được điểm A.
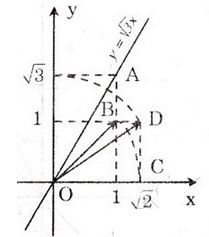

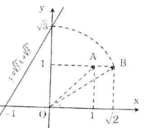
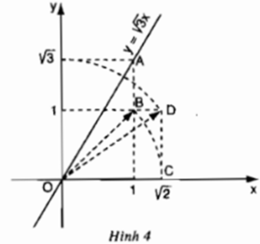
- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
![]()
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
![]()
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.

Bài giải:
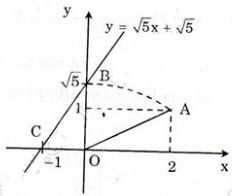
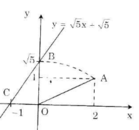
Hình bên diễn tả cách dựng đoạn thẳng có độ dài bằng √5.
Đồ thị hàm số y = √5 x + √5 đi qua hai điểm A(0; √5) và B(-1; 0).

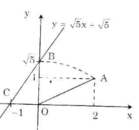
Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
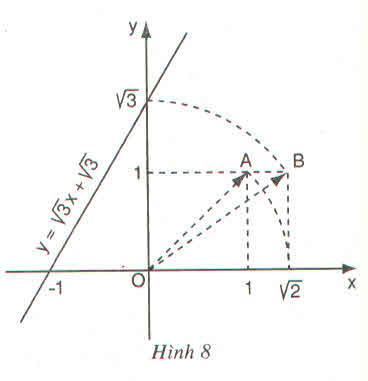
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
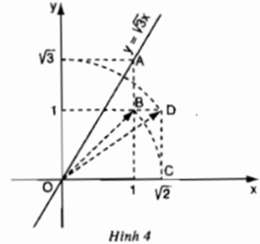
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.

a) Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
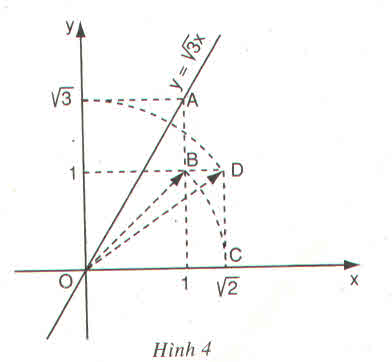
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x^2-x-4=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-8=0\\y=x+4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-4\right)\left(x+2\right)=0\\y=x+4\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(4;8\right);\left(-2;2\right)\right\}\)
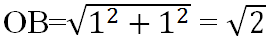
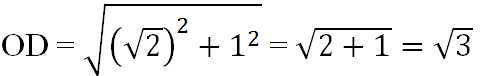


- Cách vẽ:
+ Cho x = 1 ta được y = √3.1 = √3
+ Dựng điểm A(1; √3 ). Vẽ đường thẳng qua O, A được đồ thị hàm số y = √3 x.
- Các bước vẽ đồ thị hàm số y = √3 x.
+ Dựng điểm B(1; 1). Vẽ OB ta được
+ Dựng điểm √2 trên trục hoành Ox: vẽ cung tròn bán kính OC = √2, cắt Ox tạ điểm có hoành độ là √2.
+ Dựng điểm D(√2; 1). Vẽ OD ta được
+ Dựng điểm √3 trên trục tung Ox: Vẽ cung tròn bán kính OD = √3 cắt Oy tại điểm có tung độ là √3.
+ Dựng điểm A(1; √3)
+ Vẽ đường thẳng O, A ta được đồ thị hàm số y = √3 x.