Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 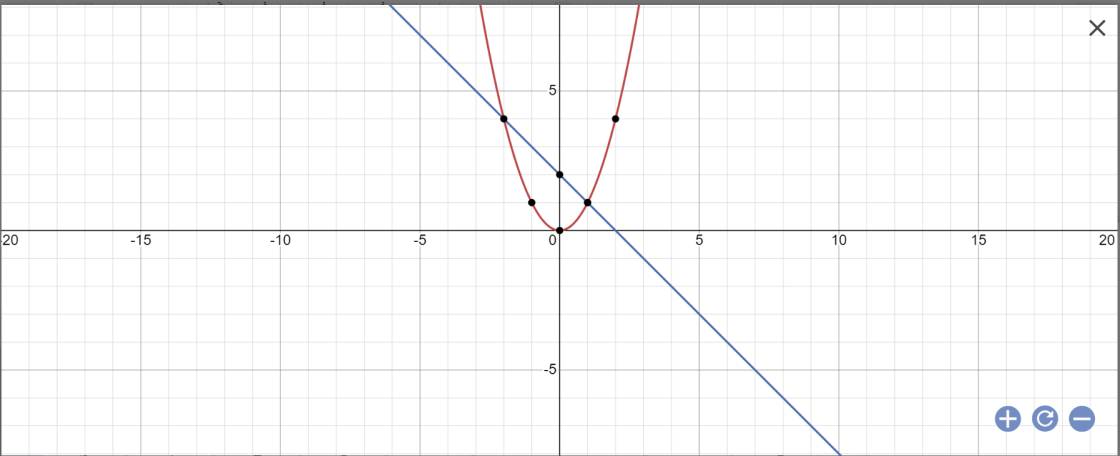
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

a)
\(\left(P\right):y=x^2\)
Ta có bảng
| x | -2 | -1 | 0 | 1 | 2 |
| y | 4 | 1 | 0 | 1 | 4 |
Vậy đồ thị hàm số \(y=x^2\) là một parabol lần lượt đi qua các điểm
\(\left(-2;4\right),\left(-1;1\right),\left(0;0\right),\left(1;1\right),\left(2;4\right)\)
Bạn tự vẽ nhé
\(\left(d\right):y=-2x+3\)
Cho \(y=0\Rightarrow x=\dfrac{3}{2}\Rightarrow A\left(\dfrac{3}{2};0\right)\in Ox\)
Cho \(x=0\Rightarrow y=3\Rightarrow B\left(0;3\right)\in Oy\)
Vẽ đường thẳng AB ta được đths \(y=-2x+3\)
Bạn tự bổ sung vào hình vẽ nhé
b) Xét PTHĐGĐ của \(\left(P\right),\left(d\right)\) là nghiệm của phương trình
\(x^2=-2x+3\\ \Leftrightarrow x^2+2x-3=0\)
Xét \(a+b+c=1+2-3=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-3\end{matrix}\right.\)
Với `x=1 => y=x^2 = 1`
Với `x=2 => y=x^2 = 4`
Vậy tọa độ giao điểm của \(\left(P\right),\left(d\right)\) là 2 điểm \(\left(1;1\right)\) và \(\left(2;4\right)\)

Theo Cô si 4x+\frac{1}{4x}\ge24x+4x1≥2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1=1⇔x=41). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x+3+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x+3+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x+1+2014=x+1(2x−1)2+201

a) tự vẽ
b) Ta có phương trình hoành độ giao điểm của đồ thị hàm số (P) và đường thẳng (d) là:
2x2 = x + 3
<=> 2x2 - x - 3 = 0
Do a - b + c = 2 + 1 - 3 = 0
=> phương trình có 2 nghiệm phân biệt x1 = -1; x2 = 3/2
Với x = -1 => y = -1 + 3 = 2 => tọa độ giao điểm là (-1;2)
x = 3/2 => y = 3/2 + 3 = 9/2 => tọa độ giao điểm là (3/2; 9/2)

1) Vẽ hai đồ thị ( P ) và ( d ) trên cùng một mặt phẳng tọa độ.
* y = − 1 2 x 2 Hàm số xác định với mọi x ∈ ℝ Bảng giá trị
Nhận xét: Đồ thị hs là một parabol đi qua gốc tọa độ,nhận trục tung làm trục đối xứng nằm phía dưới trục hoành,O là điểm cao nhất *y=x-4 Đồ thị hs là đường thẳng đi qua hai điểm (0;-4) và (4;0) |
|
2)Hoành độ giao điểm của (P) và (d) là nghiệm của phương trình
−
1
2
x
2
=
x
−
4
⇔
x
2
−
2
x
−
8
=
0
Δ ' = 1 + 8 = 9 > 0 nên phương trình có 2 nghiệm phân biệt x1=2;x2=-4
x1=2 => y1=-2 ; x2=-4 => y2=-8
Vậy tọa độ giao điểm của (P) và (d) là (2;-2) và (-4;-8)

a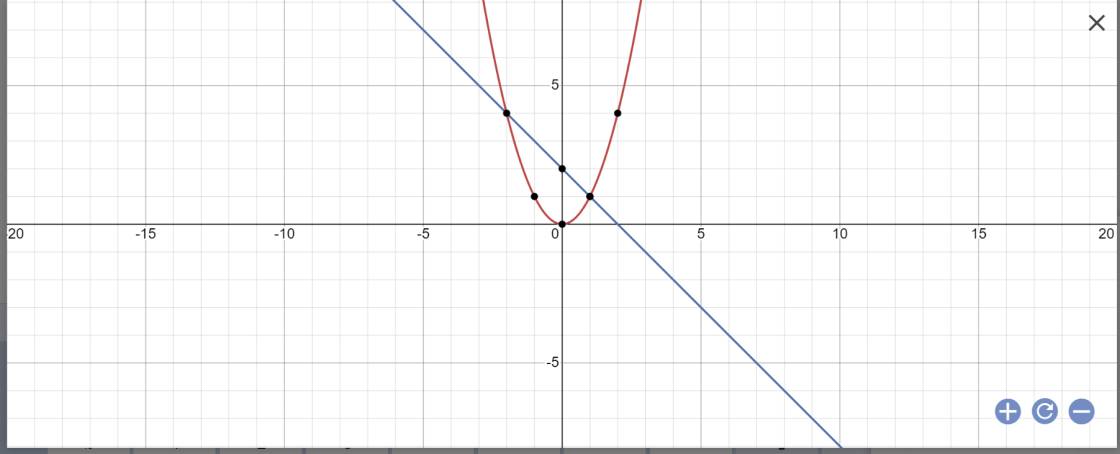
b:
PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1
a: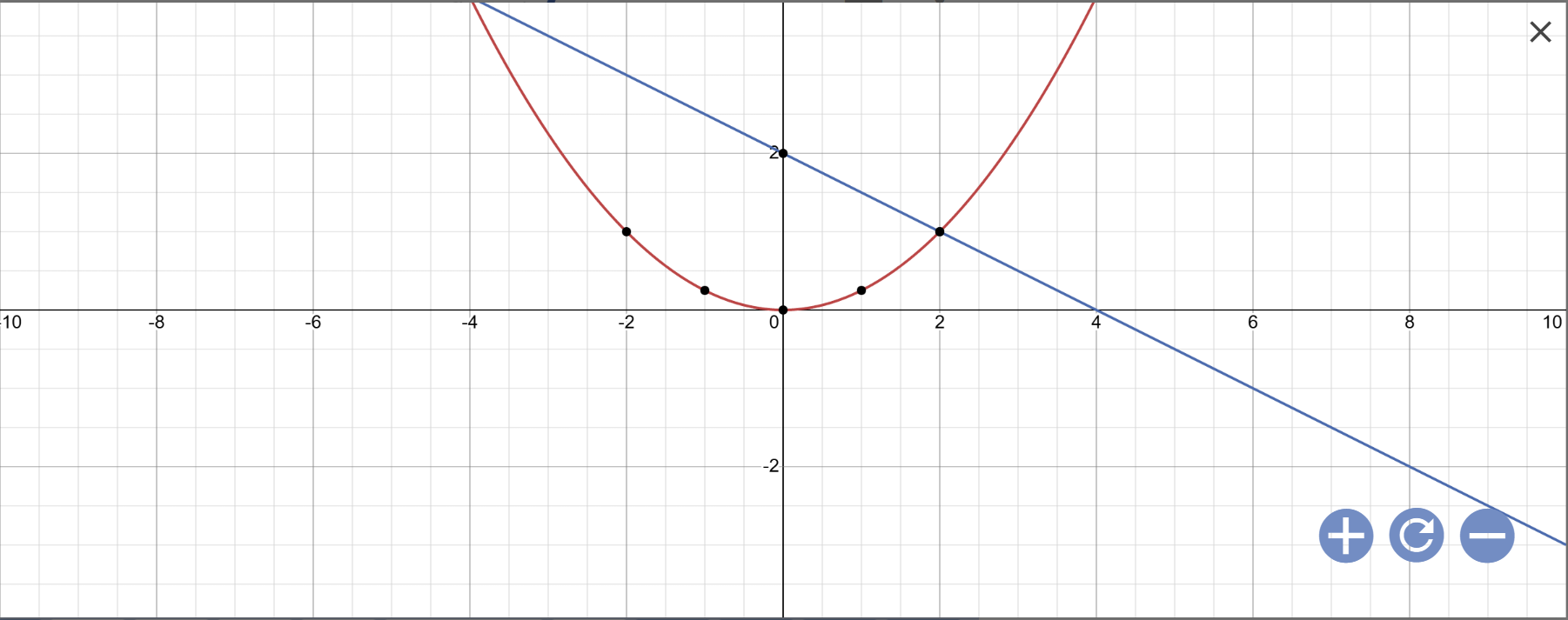
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{4}x^2=-\dfrac{1}{2}x+2\)
=>\(x^2=-2x+8\)
=>\(x^2+2x-8=0\)
=>(x+4)(x-2)=0
=>\(\left[{}\begin{matrix}x+4=0\\x-2=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-4\\x=2\end{matrix}\right.\)
Khi x=-4 thì \(y=-\dfrac{1}{2}\cdot\left(-4\right)+2=2+2=4\)
Khi x=2 thì \(y=-\dfrac{1}{2}\cdot2+2=-1+2=1\)
Vậy: Tọa độ giao điểm của (P) và (d) là A(-4;4); B(2;1)