Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Vì (d) đi qua A(3;-4) và (0;2) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}3a+b=-4\\b=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)
b: vì (d)//y=-4x+4 nên a=-4
Vậy:(d): y=-4x+b
Thay x=-2 và y=0 vào (d), ta được:
b+8=0
hay b=-8

Thay \(x=0;y=3\Leftrightarrow c=3\Leftrightarrow\left(P\right):y=ax^2-x+3\)
Vì (P) có trục đx là \(\dfrac{1}{2}\Leftrightarrow-\dfrac{\left(-1\right)}{a}=\dfrac{1}{2}\Leftrightarrow a=2\)
Vậy \(\left(P\right):y=2x^2-x+3\)

Ta có: \(y=x^2-2x+1\), có: \(a=1>0;b=-2;c=1\)
+ Tập xác định: \(D=R\)
+ Nghịch biến trên: \(\left(-\infty;1\right)\); đồng biến trên \(\left(1;+\infty\right)\)
Bảng biến nhiên:
| x | \(-\infty\) 1 \(+\infty\) |
| y | \(+\infty\) → 0 → \(-\infty\) |
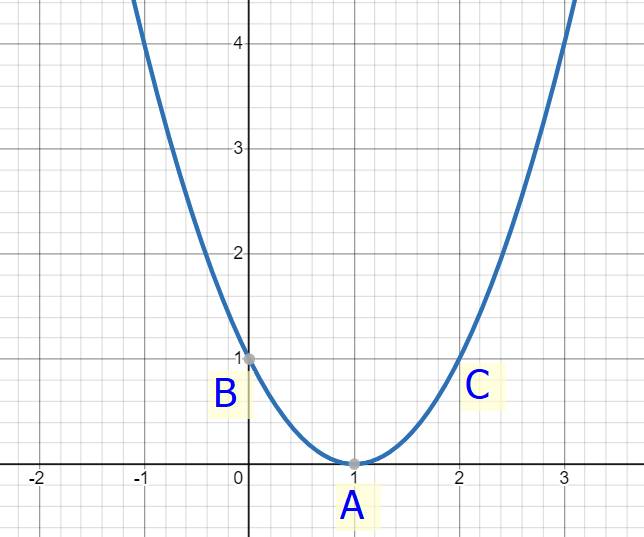
+ Đồ thị hàm số parabol có:
Đỉnh: \(A\left(1;0\right)\)
Trục đối xứng là đường thẳng x = 1
Giao điểm với Oy tại \(B\left(0;1\right)\), điểm đối xứng với B qua đường thẳng x = 1 là \(C\left(2;1\right)\)
Đi qua các điểm \(\left(-1;4\right);\left(3;4\right)\)

b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2-4x+1=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x^2-6x+5=0\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-5\right)=0\\y=2x-4\end{matrix}\right.\)
\(\Leftrightarrow\left(x,y\right)\in\left\{\left(1;-2\right);\left(5;6\right)\right\}\)
c: Điểm M,N ở đâu vậy bạn?

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2

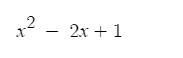
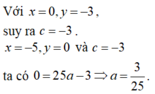
Gọi công thức của hàm số bậc hai là \(y=ax^2+bx+c\)
Trục đối xứng là x=3 nên \(-\dfrac{b}{2a}=3\)
=>b=-2a
Thay x=0 và y=-16 vào (d), ta được:
\(a\cdot0^2+b\cdot0+c=-16\)
=>c=-16
=>\(y=ax^2+bx-16\)
Thay x=-2 và y=0 vào (d), ta được:
\(a\cdot\left(-2\right)^2+b\left(-2\right)-16=0\)
=>4a-2b-16=0
=>\(4a-2\cdot\left(-2a\right)=16\)
=>8a=16
=>a=2
=>b=-2a=-4
Vậy: Công thức cần tìm là \(y=2x^2-4x-16\)