Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy pt hoành độ giao điểm d và (P), ví dụ:
\(2x^2-5x+3=x+2\)
\(\Leftrightarrow2x^2-6x+1=0\)
Bấm máy pt này, nếu nó có nghiệm kép thì đấy là đáp án đúng
Kiểm tra thì D là đáp án đúng

1) Hai đồ thị gọi là đối xứng với nhau qua trục hoành nếu f(x)+f(x)'=0
Do:
f(x)=x-2,f(x)'=2-x và f(x)+f(x)'=0=>Chúng đối xứng với nhau qua trục hoành.

Thay \(x=0;y=3\Leftrightarrow c=3\Leftrightarrow\left(P\right):y=ax^2-x+3\)
Vì (P) có trục đx là \(\dfrac{1}{2}\Leftrightarrow-\dfrac{\left(-1\right)}{a}=\dfrac{1}{2}\Leftrightarrow a=2\)
Vậy \(\left(P\right):y=2x^2-x+3\)

a: ĐKXĐ: x^2-2x<>0 và x^2-1>0
=>(x>1 và x<>2) hoặc x<-1
b: ĐKXĐ: x+1>0 và 5-3x>0
=>x>-1 và 3x<5
=>-1<x<5/3
c: DKXĐ: 5x+3>=0 và 3-x>0
=>x>=-3/5 và x<3
=>-3/5<=x<3
d: ĐKXĐ: 4-x^2>0 và 1+x>=0
=>x^2<4 và x>=-1
=>-2<x<2 và x>=-1
=>-1<=x<2
e: ĐKXĐ: 2-3x<>0 và 1-6x>0
=>x<>2/3 và x<1/6
=>x<1/6

a. Với $x_1, x_2\in\mathbb{R}$ thỏa $x_1\neq x_2$ thì:
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{-2(x_1^2-x_2^2)+(x_1-x_2)}{x_1-x_2}=1-2(x_1+x_2)\)
Với $x_1,x_2> \frac{1}{4}$ thì $A< 0$ nên hàm số nghịch biến trên $(\frac{1}{4}; +\infty)$
Với $x_1,x_2< \frac{1}{4}$ thì $A>0$ nên hàm số đồng biến trên $(-\infty; \frac{1}{4})$
b. TXĐ: $D=(-\infty; 2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2-x_1}-\sqrt{2-x_2}}{x_1-x_2}=\frac{-1}{\sqrt{2-x_1}+\sqrt{2-x_2}}< 0\)
Vậy hàm số nghịch biến trên tập xác định $(-\infty;2]$
c. TXĐ: $D=[0;2]$
\(A=\frac{f(x_1)-f(x_2)}{x_1-x_2}=\frac{\sqrt{2x_1-x_1^2}-\sqrt{2x_2-x_2^2}}{x_1-x_2}=\frac{2-(x_1+x_2)}{\sqrt{2x_1-x_1^2}+\sqrt{2x_2-x_2^2}}\)
Nếu $x_1,x_2\in (1;2)$ thì $A<0$ nên hàm số nghịch biến trên $(1;2)$
Nếu $x_1,x_2\in (0;1)$ thì $A>0$ nên hàm số nghịch biến trên $(0;1)$

Pt hoành độ giao điểm:
\(-x^2+2x+3=-2x+1\)
\(\Leftrightarrow x^2-4x-2=0\Rightarrow\left[{}\begin{matrix}x=2+\sqrt{6}\Rightarrow y=-3-2\sqrt{6}\\x=2-\sqrt{6}\Rightarrow y=-3+2\sqrt{6}\end{matrix}\right.\)
Vậy tọa độ giao điểm là: \(\left(2+\sqrt{6};-3-2\sqrt{6}\right)\)
Và \(\left(2-\sqrt{6};-3+2\sqrt{6}\right)\)
\(\left(P\right):y=-x^2+2x+3\\ \left(d\right):y=-2x+1\)
xét phương trình hoành độ giao điểm của (P) và (d)
\(-x^2+2x+3=-2x+1\)
\(< =>-x^2+4x+2=0\)
\(< =>\left[{}\begin{matrix}x=2+\sqrt{6}\\x=2-\sqrt{6}\end{matrix}\right.\)
thay vào (d) => \(\left[{}\begin{matrix}x=2+\sqrt{6}=>y=-3-2\sqrt{6}\\x=2-\sqrt{6}=>y=-3+2\sqrt{6}\end{matrix}\right.\)
vậy ...

1: Theo đề, ta có:
-b/2*(-1)=5/2
=>-b/-2=5/2
=>b=5
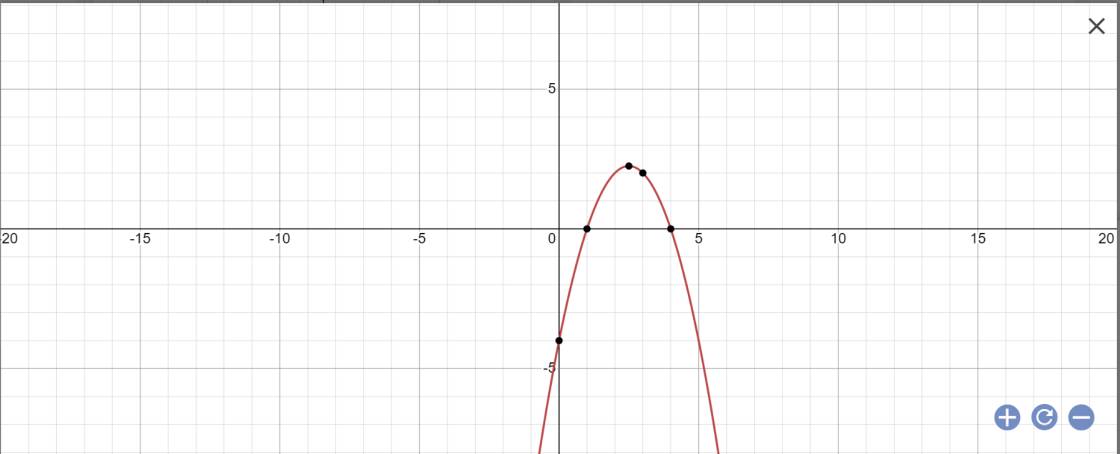
2: y=-x^2+5x-4

Trục đối xứng của parabol là \(x=-\frac{b}{2a}\Rightarrow x=-\frac{6}{2.2}=-\frac{3}{2}\)
Chọn A
cho em hỏi sao không phải đáp án B ạ ???