Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Áp dụng công thức: G = 25/f => f = 25/G = 25/5 = 5cm

Áp dụng công thức: G = 25/f => f = 25/G = 25/2,5 = 10cm = 1dm
=> Chọn D

MÌNH THAM KHẢO NHÉ
a) Xét △ABO và △A′B′O có:
ABOˆ=A′B′Oˆ=900
BOAˆ=B′OA′ˆ (hai góc đối đỉnh)
⇒ Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
⇒ \(\frac{A'B'}{AB}=\frac{B'O}{BO}\)
⇒ Độ phóng đại ảnh \(k=\frac{A'B'}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự: Hai tam giác A'B'F' và IOF' là hai tam giác đồng dạng
⇒\(\text{ }\frac{B'F'}{OF'}=\frac{A'B'}{IO}=\frac{d'}{d}\)
Áp dụng tính chất của tỉ lệ thức: \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)
⇒\(\frac{1}{f}=\frac{1}{d}=\frac{1}{f'}\)
CÓ MẤY CÁI KÍ HIỆU GÓC, MÌNH KHÔNG BIẾT VIẾT, BẠN THÔNG CẢM
a) Xét \(\Delta ABO\) và \(\Delta A'B'O'\)
\(ABO=A'B'O=90^0\)
\(BOA=B'O'A\)( hai góc đối đỉnh )
\(\Rightarrow\)Hai tam giác ABO và A'B'O là hai tam giác đồng dạng
\(\Rightarrow\frac{A'B}{AB}=\frac{B'O}{BO}\)
\(\Rightarrow\)Độ phóng đại ảnh : \(k=\frac{A'B}{AB}=\frac{h'}{h}=\frac{d'}{d}\)
b) Tương tự : Hai tam giác A'B'F và IOF' là hai tam giác đồng dạng
\(\Rightarrow\frac{B'F'}{OF}=\frac{A'B}{TO}=\frac{d'}{d}\)
Dựa vào tính chất của tỉ lệ thức : \(\frac{B'F'+OF'}{OF'}=\frac{d'+d}{d}\)hay \(\frac{d'}{f}=\frac{d'+d}{d}\)

a. Thấu kính này là TLHT vì ảnh ngược chiều vs vật...cho ảnh thật,,...
b. hình tự vẽ...
f= OF = OF'= 4.8 cm

a) vì là TKHT mà theo đề thì ta có d (tức là OA) < f ,=> ảnh ảo, cùng chiều và lớn hơn vật
b)Xét tam giác OAB đồng dạng vs ta, giác OA'B'
=> h/h' = d/d' (AB/A'B'=OA/OA')..........(1)
xét tam giac F'OI đồng dạng vs tgiac F'A'B'
=> h/h' = f/(f+d') (( OI/A'B' = FO/(FO+FA')))..........(2)
từ 1 và 2 => d/d' =f/(f+d')
chia 2 vế cho dd'f => 1/d =1/f + 1/d'
theo đề có d và f => d'=12
thế d'=12, d=6, h=1 vào (1)
=>h'=2
F' A O A' B' I
Áp dụng công thức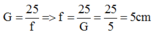
→ Đáp án B