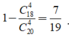Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/
a/ TH1: Lấy 1 sp loại A từ lô I có: \(C^1_3\) (cách)
Lấy 1 sp từ 4 sp còn lại từ lô II có: \(C^1_4\) (cách)
\(\Rightarrow C^1_3.C^1_4\) (cách)
TH2: Lấy 1 sp loại A từ lô II có: \(C^1_6\) (cách)
Lấy 1 sp từ 7 sp còn lại từ lô I có: \(C^1_7\) (cách)
\(\Rightarrow C^1_6.C^1_7\) (cách)
Không gian mẫu: \(n\left(\Omega\right)=C^1_{10}.C^1_{10}\)
\(\Rightarrow p\left(M\right)=\dfrac{C^1_6.C^1_7+C^1_3.C^1_4}{C_{10}^1.C^1_{10}}=0,54\)
b/ TH1: Lấy 1 sp loại A từ lô I: \(C^1_3\) (cách)
Lấy 1 sp loại A từ lô II: \(C^1_6\) (cách)
\(\Rightarrow C^1_3.C^1_6\) (cách)
TH2: Lấy 1 sp từ 7 sp còn lại trong lô I: \(C^1_7\) (cách)
Lấy 1 sp từ 4 sp còn lại trong lô II: \(C^1_4\) (cách)
\(\Rightarrow C^1_7.C^1_4\) (cách)
\(\Rightarrow p\left(O\right)=\dfrac{C_3^1.C_6^1+C^1_7.C^1_4}{C^1_{10}.C^1_{10}}=...\)
Bài 2 mình ko chắc nên ko làm nhé :(

Đáp án C
Phương pháp giải:
Chia trường hợp của biến cố, áp dụng các quy tắc đếm cơ bản tìm số phần tử của biến cố
Lời giải:
Lấy 6 sản phẩm từ 20 sản phẩm lô hàng có C 20 6 = 38760 cách ⇒ n ( Ω ) = 38760
Gọi X là biến cố 6 sản phẩm lấy ra có không quá 1 phế phẩm. Khi đó, ta xét các trường hợp sau:
TH1. 6 sản phẩm lấy ra 0 có phế phẩm nào => có C 16 6 = 8008 cách
TH2. 6 sản phẩm lấy ra có duy nhất 1 phế phẩm => có C 16 5 . C 4 1 = 17472 cách
Suy ra số kết quả thuận lợi cho biến cố X là n(X) = 8008 + 17472 = 25480
Vậy xác suất cần tính là
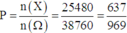

Số phần tử của không gian mẫu: \(\left|\Omega\right|=C^6_{20}\)
a) Gọi A là biến cố: "Tất cả đều là chính phẩm."
Ta thấy \(\left|A\right|=C^6_{15}\)
\(\Rightarrow P\left(A\right)=\dfrac{\left|A\right|}{ \left|\Omega\right|}=\dfrac{C^6_{15}}{C^6_{20}}=\dfrac{1001}{7752}\)
b) Gọi B là biến cố: "Tất cả đều là phế phẩm."
Rõ ràng \(\left|B\right|=0\) (vì chỉ có 5 phế phẩm nhưng ta chọn tới 6 sản phẩm nên không thể có chuyện cả 6 sản phẩm được chọn đều là phế phẩm) \(\Rightarrow P\left(B\right)=0\)
c) Gọi C là biến cố: "Có ít nhất 3 chính phẩm."
\(P_i\) là biến cố: "Có đúng \(i\) chính phẩm." \(\left(3\le i\le6\right)\)
Do \(P_i\) đôi một rời nhau và \(C=\cup^6_{i=3}P_i\) nên \(\left|C\right|=\sum\limits^6_{i=3}\left|P_i\right|\)
Ta thấy \(\left|P_i\right|=C^i_{15}.C^{6-i}_5\) \(\Rightarrow\sum\limits^6_{i=3}\left|P_i\right|=\sum\limits^6_{i=3}C^i_{15}.C^{6-i}_5=38220\)
hay \(\left|C\right|=38220\)
Từ đó \(P\left(C\right)=\dfrac{\left|C\right|}{\left|\Omega\right|}=\dfrac{38220}{C^6_{20}}=\dfrac{637}{646}\)

Chọn D
Số phần tử không gian mấu bằng số cách lấy ra 4 sản phẩm từ 20 sản phẩm là: C 20 4 (cách)
Cách 1: Để lấy ra 4 sản phẩm có sản phẩm lỗi ta chia các trường hợp:
TH1: Lấy được 3 sản phẩm tốt và 1 sản phẩm lỗi, ta có: C 18 3 . C 2 1 (cách)
TH2: Lấy được 2 sản phẩm tốt và 2 sản phẩm lỗi, ta có: C 18 2 . C 2 2 (cách)
Vậy xác suất cần tìm là: 
Cách 2: Xét biến cố đối:
Số cách lấy ra 4 sản phẩm không có sản phẩm lỗi C 18 4 (cách)
Vậy xác suất cần tìm là: