
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(S_{OMN}=\frac{a^2\sqrt{3}}{4}\Rightarrow OM=MN=a\)
Gọi P;Q lần lượt là trung điểm của AB, CD \(\Rightarrow\frac{MN}{PQ}=\frac{SM}{SP}=\frac{2}{3}\) (theo tính chất trọng tâm và định lý talet)
\(\Rightarrow AB=PQ=\frac{3}{2}MN=\frac{3a}{2}\)
Trong tam giác vuông OPM, ta có \(OM^2=OP^2+MP^2\)
\(\Rightarrow MP=\sqrt{OM^2-OP^2}=\sqrt{OM^2-\left(\frac{AB}{2}\right)^2}=\frac{a\sqrt{7}}{4}\)
Mà \(MP=\frac{1}{3}SP\) (t/c trọng tâm) \(\Rightarrow SP=\frac{3a\sqrt{7}}{4}\)
\(\Rightarrow SA=\sqrt{SP^2-AP^2}=\sqrt{SP^2-\left(\frac{AB}{2}\right)^2}=\frac{3a\sqrt{6}}{4}\)
Bạn tự thay vào tính V nhé
Cho tứ diện đều ABCD. Hạ đường cao AH của tứ diện thì do các đường xiên AB, AC, AD bằng nhau nên các hình chiếu của chúng: HB, HC, HD bằng nhau. Do BCD là tam giác đều nên H là trọng tâm của tam giác BCD.
Do đó BH =Từ đó suy ra AH2 = a2 – BH2 =
Nên AH = Thể tích tứ diện đó V=
#Hỏi cộng đồng OLM
#Toán lớp 12


Đáp án C.
Gắn hệ trục tọa độ Oxyz, với O(0;0;0) là trung điểm của AB => OC= 3
Khi đó
![]()
![]()
![]()
![]()
⇒ x 2 + ( y + 1 ) 2 + z 2 + x 2 + ( y - 1 ) 2 + z 2 + 2 ( x - 3 ) 2 + 2 y 2 + 2 z 2 = 12
![]()
![]()
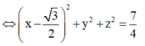
Vậy tập hợp các điểm M là một mặt cầu có bán kính
R
=
7
2





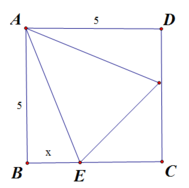
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.