
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HN
2

Các câu hỏi dưới đây có thể giống với câu hỏi trên
QN
0

HS
1


AN
30 tháng 10 2017
Hoành độ đỉnh: \(\dfrac{-b}{2a}=-\dfrac{-2}{2}=1\)
a > 0 nên đồ thị hướng lên
Vậy HS đồng biến trong khoảng (1;+\(\infty\)) -> Chọn A
LT
3

AN
30 tháng 10 2017
Đường thẳng y = ax + b đi qua A( -1; 2) và B( 2; -3)
Nên có hpt: \(\left\{{}\begin{matrix}-a+b=2\\2a+b=-3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{5}{3}\\b=\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(y=-\dfrac{5}{3}x+\dfrac{1}{3}\)
-> Chon B
AN
30 tháng 10 2017
Câu 9: ĐKXĐ: \(3-2x\ge0\)
\(\Leftrightarrow x\le\dfrac{3}{2}\)
-> Chọn B
Câu 10: Bấm máy là ra.
NT
0

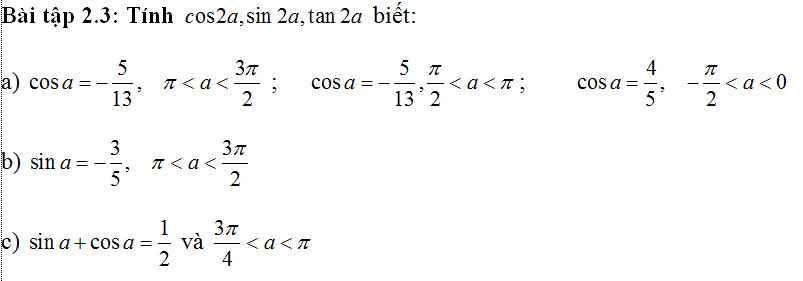








 mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha
mượn cái ngầu lòi của hai người này ới đấy đi học oln hahaha

a.
\(\pi< a< \dfrac{3\pi}{2}\Rightarrow sina< 0\)
\(\Rightarrow sina=-\sqrt{1-cos^2a}=-\dfrac{12}{13}\)
\(cos2a=cos^2a-sin^2a=\left(-\dfrac{5}{12}\right)^2-\left(-\dfrac{12}{13}\right)^2=...\)
\(sin2a=2sina.cosa=...\)
\(tan2a=\dfrac{sin2a}{cos2a}=...\)
//
\(\dfrac{\pi}{2}< a< \pi\Rightarrow sina>0\Rightarrow sina=\sqrt{1-cos^2a}=\dfrac{12}{13}\)
\(cos2a=cos^2a-sin^2a=...\) ; \(sin2a=2sina.cosa\) ; \(tan2a=\dfrac{sin2a}{cos2a}\) ...
//
\(-\dfrac{\pi}{2}< a< 0\Rightarrow sina< 0\Rightarrow sina=-\sqrt{1-cos^2a}=-\dfrac{3}{5}\)
Thay vào tính cos2a, sin2a, tan2a tương tự như trên
b.
\(\pi< a< \dfrac{3\pi}{2}\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
Tính tương tự câu a
c.
\(\dfrac{3\pi}{4}< a< \pi\Rightarrow\dfrac{3\pi}{2}< 2a< 2\pi\Rightarrow cos2a>0\)
\(sina+cosa=\dfrac{1}{2}\Rightarrow\left(sina+cosa\right)^2=\dfrac{1}{4}\)
\(\Rightarrow1+2sina.cosa=\dfrac{1}{4}\Rightarrow1+sin2a=\dfrac{1}{4}\)
\(\Rightarrow sin2a=-\dfrac{3}{4}\)
\(cos2a=\sqrt{1-sin^22a}=\dfrac{\sqrt{7}}{4}\)
\(tan2a=\dfrac{sin2a}{cos2a}=...\)