Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Bước sóng λ = v / f = 1 c m
Vì C dao động với biên độ cực đại và giữa điểm C và đường turng trực của AB còn có hai dãy cực đại khác nên C thuộc đường cực đại bậc 3
⇒ C A − C B = k λ = 3 c m
Mặt khác C A − C B = 2 A B − A B = 2 − 1 A B
⇒ 2 − 1 A B = 3 c m ⇒ A B = 3 2 − 1 c m
Vậy số điểm cực đại trên đường thẳng nối hai nguồn là:
2 A B λ + 1 = 2 3 2 − 1 + 1 = 15 đ i ể m

Đáp án B
Phương trình dao động của hai nguồn u = A cos ω t
Phương trình dao động của điểm M thuộc CO, cách nguồn khoảng d là: u M = 2 A cos ω t − 2 π d λ
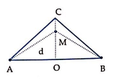
Vì điểm M dao động ngược pha với nguồn nên:
Δ φ = 2 π d λ = 2 k + 1 π ⇒ d = 2 k + 1 λ 2 = 2 k + 1 2 , 5 2 = 2 k + 1 .1 , 25
Mà A O ≤ d ≤ A C ⇒ A B 2 ≤ 2 k + 1 .1 , 25 ≤ A B 2 2 + O C 2
⇔ 12 ≤ 2 k + 1 1 , 25 ≤ 15 ⇒ 4 , 3 ≤ k ≤ 5 , 5 ⇒ k = 5
Vậy trên đoạn CO có 1 điểm dao động ngược pha với nguồn

Dao động tổng hợp x = x1 + x2
+ Khi x2 = 0 thì x1 = x - x2 = \(-5\sqrt{3}\)
+ Khi x1 = - 5 thì x2 = x - x1 = -2 + 5 = 3
Giả sử pt \(x_1=10\cos\left(\omega t\right)\) thì \(x_2=A_2\cos\left(\omega t+\varphi\right)\) (với \(\left|\varphi\right|<\frac{\pi}{2}\))
Theo giả thiết ta có:
\(\begin{cases}10\cos\left(\omega t\right)=-5\sqrt{3}\\A_2\cos\left(\omega t+\varphi\right)=0\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t\right)=-\frac{\sqrt{3}}{2}\\\cos\left(\omega t+\varphi\right)=0\end{cases}\)
cos O M1 M2 -√3/2 60°
Do \(\left|\varphi\right|<\frac{\pi}{2}\) nên ta chỉ có trường hợp như hình trên thỏa mãn, nghĩa là ta tìm đc \(\varphi=-\frac{\pi}{3}\)
Mặt khác: \(\begin{cases}10\cos\left(\omega t'\right)=-5\\A_2\cos\left(\omega t'+\varphi\right)=3\end{cases}\)\(\Rightarrow\begin{cases}\cos\left(\omega t'\right)=-\frac{1}{2}\\\cos\left(\omega t'+\varphi\right)=\frac{3}{A_2}\end{cases}\)
Cũng biểu diễn trên đường tròn lượng giác như trên, ta được
cos O M1 M2 -1/2 1/2
\(\Rightarrow A_2=6cm\)
Biên độ tổng hợp:
\(A^2=10^2+6^2+2.10.6.\cos\frac{\pi}{3}\Rightarrow A=14\)cm.

Đáp án B
Pha dao động của các điểm trên A C : φ = π d 1 + d 1 2 + 16 2 λ → để một điểm trên A C vuông pha với nguồn thì φ = π d 1 + d 1 2 + 16 2 λ = 2 k + 1 π 4 → d 1 + d 1 2 + 16 2 = 2 k + 1 λ 4
Với 0 ≤ d 1 ≤ 12 c m → có 3 giá trị

Đáp án D
+ Bước sóng của sóng λ = v f = 30 15 = 2 c m .
Số cực dãy cực tiểu giao thoa với hai nguồn cùng pha - 1 2 - S 1 S 2 λ ≤ k ≤ S 1 S 2 λ - 1 2
↔ - 5 , 5 ≤ k ≤ 4 , 4
Có 10 điểm ứng với k = - 5 , ± 4 , ± 3 , ± 2 , ± 1 , 0 .

Đáp án D
+ Bước sóng của sóng λ = v f = 30 15 = 2 c m .
Số cực dãy cực tiểu giao thoa với hai nguồn cùng pha
- 1 2 - S 1 S 2 λ ≤ k ≤ S 1 S 2 λ - 1 2
↔ - 5 , 5 ≤ k ≤ 4 , 4
Có 10 điểm ứng với k = - 5 , ± 4 , ± 3 , ± 2 , ± 1 , 0 .

Chọn B.
Với hai nguồn đồng bộ, điều kiện cực đại là d1 – d2 = k λ .

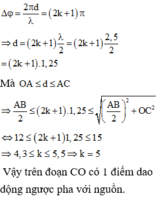
Chọn đáp án D.
Điều kiện để hai sóng cơ khi gặp nhau, giao thoa được với nhau là hai sóng phải xuất phát từ hai nguồn dao động cùng tần số, cùng phương và hiệu số pha không đổi theo thời gian.