Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Đáp số: 1/6
b) Đáp số: 937/12.
Hướng dẫn:
c) Đáp số: 2
Hướng dẫn: 
d) π/2 - 1
Hướng dẫn:
Đặt x = tan t để tính 
e) Đáp số: 27/4
Hướng dẫn: Phương trình tiếp tuyến tại (-1; -2) là y = 3x + 1. Do đó, diện tích :
Hoành độ giao điểm của hai đường là nghiệm của phương trình
Chọn D.
\(\left(x+1\right)e^x=0\Rightarrow x=-1\)
\(S=\int\limits^0_{-2}\left|\left(x+1\right)e^x\right|dx=-\int\limits^{-1}_{-2}\left(x+1\right)e^xdx+\int\limits^0_{-1}\left(x+1\right)e^xdx\)
\(=\dfrac{2e-2}{e^2}\)
1.
\(V=\pi \int ^4_1[x^{\frac{1}{2}}e^{\frac{x}{2}}]^2dx=\pi \int ^4_1(xe^x)dx\)
\(=\pi \int ^4_1xd(e^x)=\pi (|^4_1xe^x-\int ^4_1e^xdx)\)
\(=\pi |^4_1(xe^x-e^x)=\pi (3e^4)=3\pi e^4\)
2.
\(V=\pi \int ^1_0(x\sqrt{\ln (x^3+1)})^2dx=\pi \int ^1_0x^2\ln (x^3+1)dx\)
\(=\frac{1}{3}\pi \int ^1_0\ln (x^3+1)d(x^3+1)\)
\(=\frac{1}{3}\pi \int ^2_1ln tdt=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1td(\ln t))\)
\(=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1dt)=\frac{1}{3}\pi |^2_1(t\ln t-t)=\frac{1}{3}\pi (2\ln 2-1)\)
a) Diện tích hình phẳng cần tìm là:
S=2∫−1(x2+1)dx=(x33+x)∣∣2−1=6
b) Diện tích hình phẳng cần tìm là:
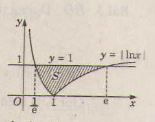
S=e∫1e| lnx |dx=e∫1e|lnx|dx+e∫1|lnx|dx=−1∫1elnxdx+e∫1lnxdxS=∫1ee|lnx|dx=∫1ee|lnx|dx+∫1e|lnx|dx=−∫1e1lnxdx+∫1elnxdx
Mặt khác:
∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C
Do đó:
S=−1∫1elnxdx+e∫1lnxdx=1e∫1lnxdx+e∫1xdx=(xlnx−x)∣∣∣1e1+(xlnx−x)∣∣e1=2(1- \(\dfrac{1}{e}\))
Khó quá, làm mà điên não
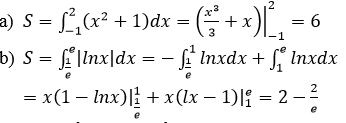
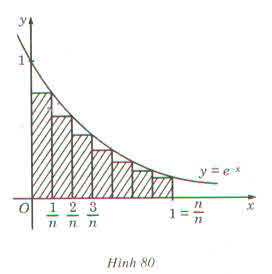
Chọn A.
Phương trình hoành độ giao điểm của hai đồ thị hàm số y = ex và trục y = 1 là: ex = 1 ⇔ x = 0
Do đó: