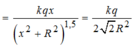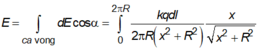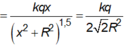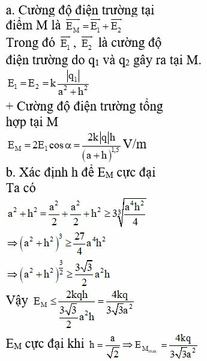Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

đáp án D
Ta chia vòng dây thành nhiều vi phân nhỏ d ℓ
điện tích của vi phân này bằng d q = q d ℓ 2 π R
phần này gây ra tại O một điện trường d E →
d E = k d q x 2 + R 2 = k q d ℓ 2 π R x 2 + R 2
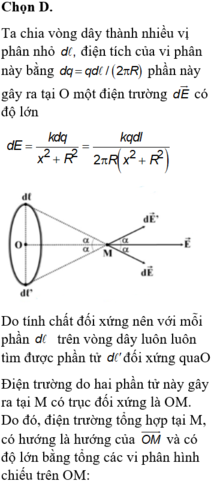
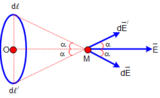
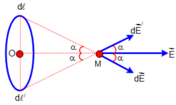
+ Do tính đối xứng nên với mỗi phần tử d ℓ trên vòng dây luôn luôn tìm được phần tử d ℓ đối xứng với O. Điện trường do hai phần tử này gây ra tại M có trục đối xứng là OM.Do đó, điện trường tổng hợp tại M, có hướng của O M → và có độ lớn bằng tổng các vi phân hình chiếu trên OM

Đáp án D
Ta chia vòng dây thành nhiều vi phân nhỏ ![]() điện tích của vi phân này bằng
điện tích của vi phân này bằng ![]() phần này gây ra tại O một điện trường
phần này gây ra tại O một điện trường ![]() có độ lớn
có độ lớn
![]()
![]()
Do tính đối xứng nên với mỗi phần tử ![]() trên vòng dây luôn luôn tìm được phần tử
trên vòng dây luôn luôn tìm được phần tử ![]() đối xứng với O. Điện trường do hai phần tử này gây ra tại M có trục đối xứng là OM
đối xứng với O. Điện trường do hai phần tử này gây ra tại M có trục đối xứng là OM
Do đó, điện trường tổng hợp tại M, có hướng của ![]() và có độ lớn bằng tổng các vi phân hình chiếu trên OM
và có độ lớn bằng tổng các vi phân hình chiếu trên OM
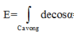
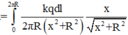
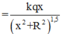

A B M C D N h P a a
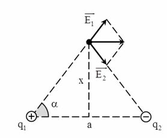
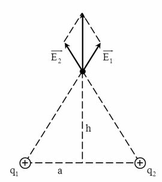
a) Vector cường độ điện trường tại M có phương và chiều được xác định như hình vẽ
Ta có \(|\overrightarrow{E_A}|=|\overrightarrow{MC}|=\frac{kq}{MA^2}=\frac{kq}{a^2+h^2}\)
\(\frac{MC}{MA}=\frac{MN}{2MP}\Rightarrow MN=\left|\overrightarrow{E_{AB}}\right|=\frac{2MC.MP}{MA}=\frac{2kqh}{\left(a^2+h^2\right)\sqrt{a^2+h^2}}\left(\frac{V}{m}\right)\)
b) Áp dụng BĐT Cauchy ta có:
\(E_{AB}=\frac{2kqh}{\sqrt{\left(a^2+h^2\right)^3}}=\frac{2kqh}{\sqrt{\left(\frac{a^2}{2}+\frac{a^2}{2}+h^2\right)^3}}\)
\(\le\frac{2kqh}{\sqrt{\left(3\sqrt[3]{\frac{a^4h^2}{4}}\right)^3}}=\frac{4kq}{3\sqrt{3}a^2}\)(không đổi)
Đạt được khi \(h=\frac{a\sqrt{2}}{2}.\)