OLM ưu đãi đặc biệt gói SVIP 18 THÁNG dành cho nhà trường, đăng kí ngay!

OLM tuyển CTV cộng đồng hỏi đáp, đăng kí ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
SG
Sách Giáo Khoa
17 tháng 4 2017

Điền phân số thích hợp vào ô trống :

a) \(\dfrac{1}{12}+.....=\dfrac{-2}{3}\)

b) \(\dfrac{-1}{3}+......=\dfrac{2}{5}\)

c) \(\dfrac{1}{4}-......=\dfrac{1}{20}\)

d) \(\dfrac{-8}{13}-......=0\)
#Hỏi cộng đồng OLM #Toán lớp 6
1
LH
Lưu Hạ Vy
17 tháng 4 2017

Coi phân số phải tìm là x rồi vận dụng quy tắc chuyển vế để tìm x.

Chẳng hạn:

\(c)\) \(\dfrac{1}{4}-x=\dfrac{1}{20}\) . Chuyển vế thì ta đc :

\(x=\dfrac{1}{5}\)

Đáp số:

\(a)-\dfrac{3}{4}\)

b) \(\dfrac{11}{15}\)

c) \(\dfrac{1}{5}\)

d) \(-\dfrac{8}{13}\)

Đúng(0)
PT
Pham Trong Bach
6 tháng 6 2017

Điền số thích hợp vào ô vuông:

1 = □ 2 = □ - 4 = □ 6 = - 8 □ = 10 □

#Hỏi cộng đồng OLM #Toán lớp 6
1
CM
Cao Minh Tâm
6 tháng 6 2017

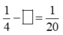
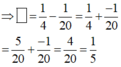
Áp dụng tính chất nhân cả tử và mẫu của một phân số với cùng một số:

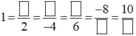
Giải bài 11 trang 11 SGK Toán 6 Tập 2 | Giải toán lớp 6

Các phân số trên đều bằng 1 nên tử số = mẫu số.

Do đó ta điền như sau:

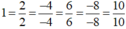
Giải bài 11 trang 11 SGK Toán 6 Tập 2 | Giải toán lớp 6

Đúng(0)
QA
Quỳnh Anh Daisy
22 tháng 7 2021
Điền số thích hợp vào ô vuông: a) \(\dfrac{1}{2}\)=\(\dfrac{ }{12}\)                       b)\(\dfrac{ }{8}\)=\(\dfrac{-28}{32}\)                        c)\(\dfrac{3}{4}\)=\(\dfrac{ }{20}\)                       d)\(\dfrac{ }{9}\)=\(\dfrac{-16}{36}\)                                 e)\(\dfrac{3}{4}\)=\(\dfrac{15}{...
Đọc tiếp

Điền số thích hợp vào ô vuông: 

a) \(\dfrac{1}{2}\)=\(\dfrac{ }{12}\)                       b)\(\dfrac{ }{8}\)=\(\dfrac{-28}{32}\)                        c)\(\dfrac{3}{4}\)=\(\dfrac{ }{20}\)           

            d)\(\dfrac{ }{9}\)=\(\dfrac{-16}{36}\)                                 e)\(\dfrac{3}{4}\)=\(\dfrac{15}{ }\)

 
#Hỏi cộng đồng OLM #Toán lớp 6
2
PV
Phạm Vĩnh Linh
22 tháng 7 2021

a)6

b,-7

c)15

d)-4

e)20

Đúng(0)
VV
Vân Vui Vẻ
22 tháng 7 2021

a) \(\dfrac{1}{2}\)=\(\dfrac{6}{12}\)       b) \(\dfrac{-7}{8}\)=\(\dfrac{-28}{32}\)      c)\(\dfrac{3}{4}\)=\(\dfrac{15}{20}\)       d) \(\dfrac{-4}{9}\)=\(\dfrac{-16}{36}\)

e) \(\dfrac{3}{4}\)=\(\dfrac{15}{20}\)

HỌC TỐT

Đúng(1)
PT
Pham Trong Bach
14 tháng 9 2019

Điền phân số thích hợp vào ô vuông:  - 8 13 - □ = 0 .
#Hỏi cộng đồng OLM #Toán lớp 6
1
CM
Cao Minh Tâm
14 tháng 9 2019

Đúng(0)
PT
Pham Trong Bach
25 tháng 4 2018

Điền phân số thích hợp vào ô vuông:  - 1 3 + □ = 2 5 .
#Hỏi cộng đồng OLM #Toán lớp 6
1
CM
Cao Minh Tâm
25 tháng 4 2018

Đúng(0)
PT
Pham Trong Bach
16 tháng 10 2019

Điền phân số thích hợp vào ô vuông:  1 12 + □ = - 2 3 .
#Hỏi cộng đồng OLM #Toán lớp 6
1
CM
Cao Minh Tâm
16 tháng 10 2019

Đúng(0)
LT
Lê Trung Hiếu
4 tháng 8 2020 - olm

Điền số thích hợp vào ô vuông:

\(\frac{1}{4}\)= \(\frac{ }{ }\); \(\frac{-3}{4}\)= \(\frac{ }{ }\); 1 = \(\frac{ }{2}\)= \(\frac{ }{-4}\)= \(\frac{ }{6}\)= \(\frac{-8}{ }\)= \(\frac{10}{ }\)


 
#Hỏi cộng đồng OLM #Toán lớp 6
1
NN
Nguyễn Nhung
VIP
4 tháng 8 2020

1/4=1/4;-3/4=-3/4;1=2/2=-4/-4=6/6=-8/-8=10/10

Đúng(0)
MY
Mình yêu các bạn trên Hoc24.vn nhiề...
27 tháng 9 2016

Cho phân số \(\frac{a}{b}>1\), m là một số tự nhiên \(\ne\) 0. Hãy điền dấu ( >, <, = ) thích hợp vào ô trống:

\(\frac{a}{b}.....\frac{a+m}{b+m}\)
#Hỏi cộng đồng OLM #Toán lớp 6
2
TT
Trần Thị Bảo Trân
27 tháng 9 2016

Ta có:

                \(\frac{a}{b}=\frac{a\times\left(b+m\right)}{b\times\left(b+m\right)}=\frac{a\times b+a\times m}{b\times b+b\times m}\)

                \(\frac{a+m}{b+m}=\frac{\left(a+m\right)\times b}{\left(b+m\right)\times b}=\frac{a\times b+m\times b}{b\times b+b\times m}\)

vì \(\frac{a}{b}>1\) nên \(a>b\), ta suy ra \(a\times m>b\times m\)

hay \(a\times b+a\times m>a\times b+m\times b\)

hay \(\frac{a\times b+a\times m}{b\times b+b\times m}>\frac{a\times b+m\times b}{b\times b+b\times m}\)

hay \(\frac{a}{b}>\frac{a+m}{b+m}\)

Đúng(0)
SG
soyeon_Tiểubàng giải
27 tháng 9 2016

Vì \(\frac{a}{b}>1\)

=> a > b

=> a.m > b.m

=> a.m + a.b > b.m + a.b

=> a.(b + m) > b.(a + m)

=> \(\frac{a}{b}>\frac{a+m}{b+m}\)

Đúng(0)
TQ
Trần Quang Hiếu
22 tháng 7 2016

Bài 1: Điền số thích hợp vào ô vuông:

a) \(\frac{7}{ }=\frac{21}{-39}\)

B) \(\frac{ }{8}=\frac{-28}{32}\)     

Bài 2 : Tìm các số nguyên x và y, biết :

a) \(\frac{x}{7}=\frac{6}{21}\)         b) \(\frac{-5}{y}=\frac{20}{28}\)          c) \(\frac{-4}{8}=\frac{x}{-10}\)
#Hỏi cộng đồng OLM #Toán lớp 6
1
PT
phan thị minh anh
22 tháng 7 2016

a. -13

b.-7

bài 2 :

a. x=2

b. y=-7

c. x=5

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP