Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hai số a và b cùng dấu.
b) Hai số a và b cùng dấu.
c) Hai số a và b trái dấu nhau.
d) Hai số a và b trái dấu nhau.

Chọn A.
Ta có : P = sin3 α + cos3 α = ( sinα + cosα) 3 - 3sin α.cosα(sinα + cosα)
Ta có (sin α + cos α) 2 = sin2α + cos2α + 2sinα.cosα = 1 + 24/25 = 49/25.
Vì sin α + cosα > 0 nên ta chọn sinα + cosα = 7/5.
Thay 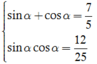 vào P ta được
vào P ta được 

Để tam thức đổi dấu 2 lần
\(\Leftrightarrow x^2-\left(m+2\right)x+8m+1=0\) có 2 nghiệm pb
\(\Leftrightarrow\Delta=\left(m+2\right)^2-4\left(8m+1\right)>0\)
\(\Leftrightarrow m^2-28m>0\Rightarrow\left[{}\begin{matrix}m>28\\m< 0\end{matrix}\right.\)

Chọn D.
Ta có ( sinα - cosα) 2 + (sinα + cosα) 2 = 2( sin2α + cos2α) = 2.
Suy ra (sinα - cosα) 2 = 2 - ( sinα + cos α) 2 = 2 - 5/4 = 3/4.
Do ![]() suy ra sinα < cosα nên sinα - cosα < 0.
suy ra sinα < cosα nên sinα - cosα < 0.
Vậy 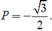

a) Mệnh đề sai;
b) Mệnh đề chứa biến;
c) Mệnh đề chứa biến;
d) Mệnh đề đúng.
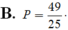
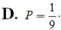
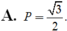
Chọn C.
Điểm cuối của α thuộc góc phần tư thứ hai nên sinα > 0 ; cosα < 0.