Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tự vẽ hình nha
1. Xét tam giác EBH có: BE=BH (gt) -> tan giác EBH cân tại B -> góc BEH = góc BHE
Ta lại có góc ABH = góc BEH + góc BHE (góc ngoài của tam giác EBH); Mà góc BEH = góc BHE (cmt) -> góc ABH = 2 góc BEH; Mà góc ABH = 2 góc ACB (gt)-> góc BEH = góc ACB ( đpcm)
2. Ta có: góc BHE = góc DHC (2 góc đối đỉnh); Mà góc BHE = góc BEH (cmt) và góc BEH = góc ACB (cmt) => góc DHC = góc ACB -> tam giác DHC cân tại D -> DH = DC ( 2 cạnh tương ứng)
Ta có: tam giác AHC vuông tại H -> góc HAC +góc ACB = 90 độ (2 góc ở đáy tam giác vuông ); Mà góc AHD + góc DHC = 90 độ và góc ACB = góc DHC (cmt) -> góc HAC = góc AHD -> tam giác AHD cân tại D => DA = DH (2 cạnh tương ứng )
Vậy DH=DC=DA
3. Ta có tam giác ABB' có: BH = B'H ( H là trung điểm BB') -> AH là đường trung tuyến lại vừa là đường cao -> tam giác ABB' cân tại A -> góc ABH = góc AB'H (2 góc ở đáy)
Xét tam giác AB'C có: góc AB'H = góc B'AC + góc ACB' (góc ngoài); Mà góc ABH = góc AB'H (cmt) -> góc ABH = góc B'AC + góc ACB ; Mà góc ABH = 2 góc ACB'
-> góc B'AC = góc ACB' => tam giác AB'C cân tại B'
4. Bạn vẽ lại hình nha: giả sử tam giác ABC vuông tại A
Xét tam giác ADE và tam giác ABC có: góc A chung và góc BEH = góc ACB (cmt) -> hai tam giác đồng dạng theo trường hợp (g.g) -> góc ADE = góc ABC (2 góc tương ứng) (1)
Ta có : góc HAD = 90 độ - góc C ( tam giác HAC vuông tại H); Mà góc ABC = 90 độ - góc C ( tam giác ABC vuông tại A) -> góc HAD = góc ABC (2)
Từ (1) và (2) -> góc ADE = góc HAD; Mà góc HAD = góc AHD nên suy ra tam giác AHD đều
Xét tam giác ADE và tâm giác HAC có: góc EAD = góc CHA = 90 độ (gt); góc ADE = góc HAC (cmt); AD = AH (tam giác AHD đều) => tam giác ADE = tam giác HAC theo trường hợp (g.c.g)
=> DE = AC (2 cạnh tương ứng) => DE2 = AC2 ; Mà AC2 = BC2 - AB2 (định lí Py-ta-go trong tam giác ABC) => DE2 = BC2 - AB2 (đpcm)
Học tốt nhé 🙋♀️🙋♀️🙋♀️💗💗💗

Giải
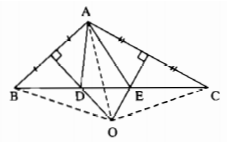
a) D thuộc đường trung trực của AB nên DA = DB (tính chất đường trung trực)
Vậy ∆ADB cân tại D.
E thuộc đường trung trực của AC nên AE = EC (tính chất đường trung trực)
Vậy ∆AEC cân tại A.
b)Vì O là giao điểm ba đường trung trực của ∆ABC nên:
OA = OB = OC
Vậy (O;OA) đi qua ba điểm A, B, C.

giúp mình với nhé mai mình thi cuối học kì I môn toán rồi. Chúc các bạn có một kì thi tốt đẹp.
đề bài sai à
câu a tam giác vuông tại A mà góc B = 90o suy ra góc C = 0o à

Bạn tự vẽ hình nha!!!
a.)Xét\(\Delta ABD\)và\(\Delta ABM\)có:
\(AD=BM\)
\(AB:\)Chung
\(\widehat{DAB}=\widehat{ABM}\left(slt\right)\)
\(\Rightarrow\Delta ABD=\Delta BAM\)
b.)Ta có:\(\Delta ABD=\Delta BAM\)(Theo a)
\(\Rightarrow\widehat{DBA}=\widehat{BAM}\)(mà 2 góc SLT)
\(\Rightarrow AM//BD\)
c.)Xét\(\Delta ADI\)và\(\Delta IMC\)có:
\(AD=CM\)
\(\widehat{DAI}=\widehat{IMC}\)
\(AI=IM\)
\(\Rightarrow\Delta AID=\Delta IMC\)
\(\Rightarrow IA=IC\)
\(\Rightarrow I\)là trung điểm của\(AC\)
\(\Rightarrow I,A,C\)thẳng hàng(đpcm)
P/s:#Study well#
O B A C O'
Lấy điểm O' sao cho \(OB\perp O'B;OB=O'B\)( O' cùng phía với C so với OB)=> O' cố định
Khi đó góc OBA = Góc O'BC( cùng phụ góc ABO')
=> \(\Delta BOA=\Delta BO'C\)( cạnh.góc.canh)
=> \(O'C=OA=1\)
Mà O' cố định
=> C thuộc đường tròn tâm O' BK=1 cố định
Để OC lớn nhất thì
C là giao của OO' với đường tròn tâm O' (C nằm ngoài OO')
ÁP dụng PItago ta có \(OO'=\sqrt{2}\)
=> \(OC=OO'+O'C=1+\sqrt{2}\)
Vậy \(MaxOC=1+\sqrt{2}\)