K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 6 2018
B=\(2\sqrt{18}-4\sqrt{32}+\sqrt{72}+3\sqrt{8}\)
\(=6\sqrt{2}-16\sqrt{2}+6\sqrt{2}+6\sqrt{2}\)
\(=2\sqrt{2}\)
TV
11 tháng 6 2018
\(B=2\sqrt{18}-4\sqrt{32}+\sqrt{72}+3\sqrt{8}\)
\(=6\sqrt{2}-16\sqrt{2}+6\sqrt{2}+6\sqrt{2}\)
\(=\sqrt{2}\left(6-16+6+6\right)\)
\(=2\sqrt{2}\)
13 tháng 7 2022
Câu 1:
\(\Leftrightarrow1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}=\dfrac{2999}{3000}\)
\(\Leftrightarrow1-\dfrac{1}{n+1}=\dfrac{2999}{3000}\)
=>n+1=3000
hay n=2999
4 tháng 6 2022
\(=\dfrac{\left(5\sqrt{a}-3\right)\left(\sqrt{a}+3\right)+\left(3\sqrt{a}+1\right)\left(\sqrt{a}-2\right)-a^2-2\sqrt{a}-8}{a-4}\)
\(=\dfrac{5a+15\sqrt{a}-3\sqrt{a}-9+3a-6\sqrt{a}+\sqrt{a}-2-a^2-2\sqrt{a}-8}{a-4}\)
\(=\dfrac{-a^2+8a+5\sqrt{a}-19}{a-4}\)
1 tháng 8 2021
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
Để \(P=\dfrac{7}{2}\) thì \(2x+2\sqrt{x}+2-7\sqrt{x}=0\)
\(\Leftrightarrow2x-4\sqrt{x}-\sqrt{x}+2=0\)
\(\Leftrightarrow2\sqrt{x}\left(\sqrt{x}-2\right)-\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{4}\end{matrix}\right.\)
TH
1
14 tháng 6 2023
\(A=\sqrt{\sqrt{7}-\sqrt{3}}-\sqrt{\sqrt{7}+\sqrt{3}}\)
=>\(A^2=\sqrt{7}-\sqrt{3}+\sqrt{7}+\sqrt{3}-2\sqrt{4}\)
=>A^2=2căn 7-4
=>A=2căn 7-4
=>\(M=\dfrac{2\left(\sqrt{7}-2\right)}{\sqrt{7}-2}=2\)
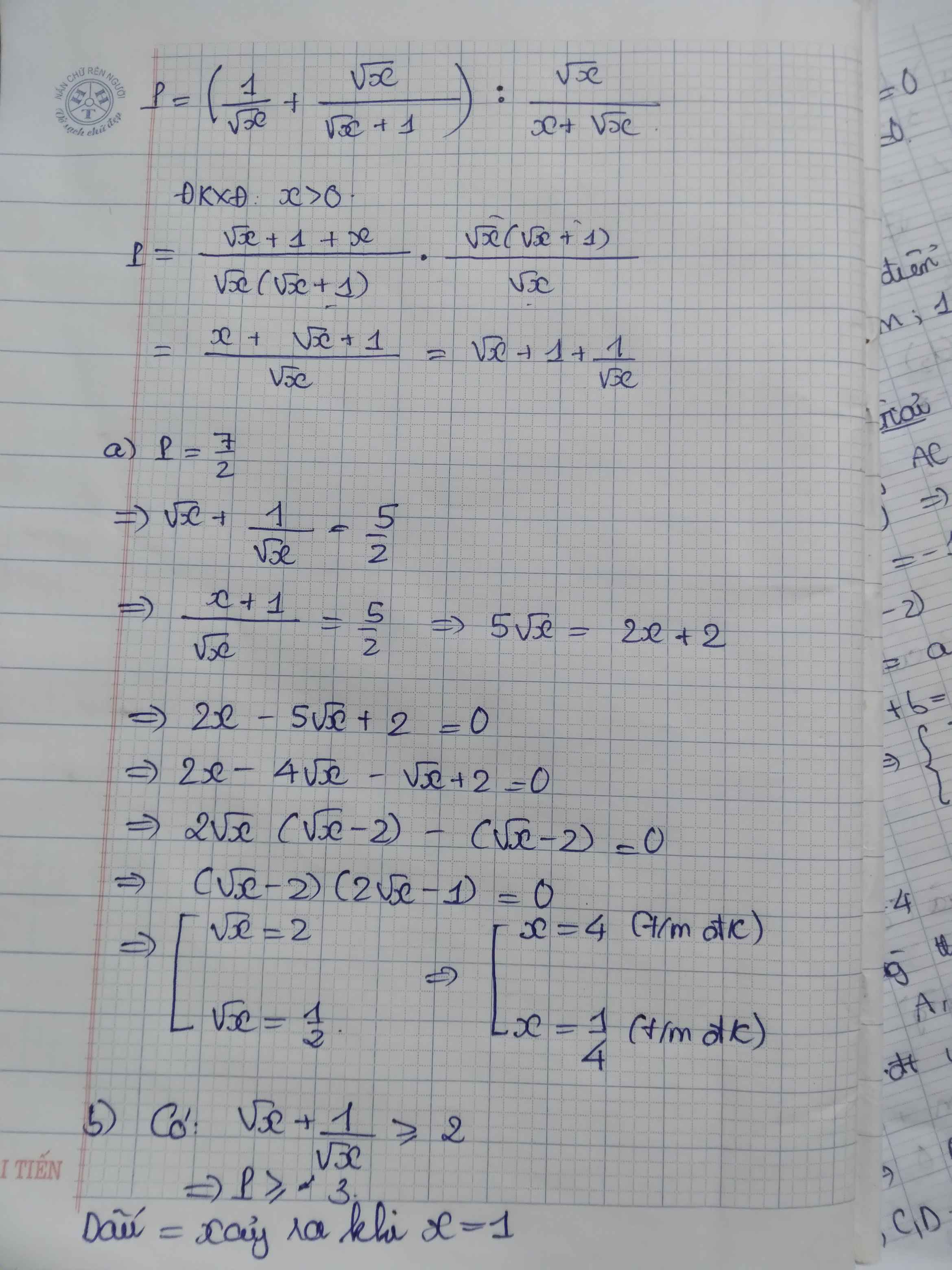
\(\dfrac{1}{\sqrt{8}+\sqrt{7}}+\sqrt{175}-2\sqrt{2}=\dfrac{\sqrt{8}-\sqrt{7}}{\left(\sqrt{8}-\sqrt{7}\right)\left(\sqrt{8}+\sqrt{7}\right)}+\sqrt{25.7}-2\sqrt{2}\)
\(=\dfrac{\sqrt{8}-\sqrt{7}}{1}+5\sqrt{7}-2\sqrt{2}=2\sqrt{2}-\sqrt{7}+5\sqrt{7}-2\sqrt{2}\)
\(=4\sqrt{7}\)