Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số thợ cần thiết là x (người),x ∈ N* , thời gian cần thiết là y (ngày), y > 0.
Coi toàn bộ công việc như một đơn vị công việc, thì một người thợ trong 1 ngày làm được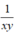 
( công việc).
Nếu giảm đi 3 người thì thời gian kéo dài 6 ngày. Như vậy, x – 3 người làm trong y + 6 ngày thì xong công việc. Do đó, ta có phương trình:
Nếu tăng thêm 2 người thì xong sớm 2 ngày. Như vậy, x + 2 người làm trong y – 2 ngày thì xong công việc. Do đó, ta có phương trình:
Từ (1) và (2) ta có hệ phương trình:
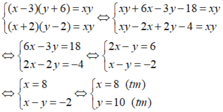
Vậy cần 8 người làm trong 10 ngày thì xong công việc.
Gọi số thợ và số ngày lần lượt là a,b
Theo đề, ta có hệ:
(a-3)(b+6)=ab và (a+2)(b-2)=ab
=>ab+6a-3b-18=ab và ab-2a+2b-4=ab
=>6a-3b=18 và -2a+2b=4
=>a=8 và b=10
- Gọi số người thợ ban đầu và số ngày cần làm theo quy định lần lượt là x (người) và y (ngày), (điều kiện cậu tự viết nhé)
- Từ đó ta có số công việc cân làm là : xy (công việc)
- Khi giảm 3 người thợ thì ta còn lại : x -3 (người)
- Khi thời gian phải kéo dài thêm 6 ngày thì tổng số ngày làm để xong việc là : y + 6 (ngày)
- Khi giảm 3 người thợ thì kéo dài thêm 6 ngày, mà số lượng công việc khong đổi nên ta có phương trình :
(x - 3).(y + 6) = xy <=> 6x - 3y = 18 (1)
/tăng thêm 2 người, xong sớm 2 ngày cũng làm tượng tự như vậy nha/ Từ đó ta có phương trình:
(x +2).(y - 2) = xy <=> -2x + 2y = 4 (2)
/từ chỗ này thì cậu tự giải hệ phương trình nha/
Gọi số thợ là x và số ngày dự định là y (x>3;y>2)
Trong một ngày một thợ làm được \(\frac{1}{xy}\) phần công việc
Theo bài ra ta có hệ pt:
\(\left\{{}\begin{matrix}\left(x-3\right)\left(y+6\right).\frac{1}{xy}=1\\\left(x+2\right)\left(y-2\right)\frac{1}{xy}=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}6x-3y-18=0\\-2x+2y-4=0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=8\\y=10\end{matrix}\right.\)
Ket qua to1 lam duoc trong thang dau la420 sp
To2 lam duoc300sp