Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Chọn ngẫu nhiên 6 học sinh trong 15 học sinh có C 15 6 cách ⇒ n Ω = C 16 5 .
Gọi X là biến cố “6 học sinh được chọn có đủ 3 khối” => biến cố đối X ¯ là “6 học sinh được chọn trong một khối hoặc hai khối”. Ta xét các trường hợp sau:
TH1. Chọn 6 học sinh từ một khối. Ta xét các trường hợp sau:
TH2. Chọn 6 học sinh từ hai khối, ta được
· 6 học sinh chọn từ khối 11 và 11 => có C 11 6 - C 6 6 cách
· 6 học sinh chọn từ khối 11 và 12 => có C 9 6 cách
· 6 học sinh chọn từ khối 12 và 10 => có C 10 6 - C 6 6 cách.
Vậy P = 1 - n X ¯ n Ω = 1 - 755 C 15 6 = 850 1001 .

xin lỗi vì đã quá trễ nhưng giải cho người khác biết =(
thì tính kgm n(Ω)= 20C3
tiếp theo mk có biến cố A : " Ba người thì trong đó ko có 1 cặp vợ chồng nào"
\(\rightarrow\overline{A}:\)" Ba người trong đó có ít nhất 1 cặp vợ chồng" ( biến cố đối)
Chọn ra 1 cặp vợ chồng từ 4 cặp : 4C1 cách
- 1 cặp đã có sẵn 2 người r mà mình đã chọn 1 cặp thì số người còn lại là 18 người
=> 18C1 cách
\(P_{\overline{A}}=\dfrac{n\overline{A}}{n\Omega}\) \(=\dfrac{4C1.18C1}{20C3}\)
=> P(A) = 1 - P(\(\overline{A}\) ) => câu D nhóa


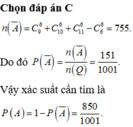

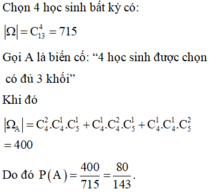
Đáp án A
Chọn 3 tiết mục bất kỳ có: Ω = C 9 3 = 84 cách. Gọi A là biến cố: “ba tiết mục được chọn có đủ cả ba khối và đủ cả ba nội dung”. Khối 10 chọn 1 tiết mục có 3 cách, khối 11 chọn 1 tiết mục khác khối 10 có 2 cách, tương tự khối 12 có 1 cách. Ta có: Ω A = 3.2.1 = 6 cách.
Vậy P = 6 84 = 1 14 .