
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có hình vẽ sau:
E D F K A B
a) Ta có \(\Delta DEF\)vuông tại E
=> ED2+EF2=DF2 ( Theo định lý Py-ta-go)
=> 82+62=DF2
=> DF2=100
=> DF=10(cm)
Vậy DF=10cm
b) Xét \(\Delta DKE\)và \(\Delta DKA\):
DK: cạnh chung
\(\widehat{EDK}=\widehat{ADK}\left(gt\right)\)
\(\widehat{DEK}=\widehat{DAK}=90^o\)
=> \(\Delta KDE=\Delta KDA\left(ch-gn\right)\)
=> DE=DA( 2 cạnh t/ứ)
=> đpcm
c) Ta có: \(\Delta DEK=\Delta DAK\)(cm câu b)
=> EK=AK( 2 cạnh t/ứ)
Xét \(\Delta EKB\)vuông tại E có: KB>KE
=> KB> AK
d) Xét \(\Delta EKB\)và \(\Delta AKF\):
\(\widehat{BEK}=\widehat{FAK}=90^o\)
EK=AK( cm câu c)
\(\widehat{EKB}=\widehat{FKB}\left(đđ\right)\)
=> \(\Delta BEK=\Delta FAK\left(g.c.g\right)\)
=> EB=AF (2 canh t/ứ)
Lại có DE=DA(cm câu b)
=> DE+EB=DA+AF
=> DB=DF
=> \(\Delta DBF\)cân ở D
=> \(\widehat{DBF}=\frac{180^o-\widehat{BDF}}{2}\left(1\right)\)
Mà \(\Delta DEA\)cân ở D(DE=DA)
=> \(\widehat{DEA}=\frac{180^o-\widehat{EDA}}{2}\left(2\right)\)
Từ (1) và (2) => \(\widehat{DBF}=\widehat{DEA}\)
Mà 2 góc này ở vị trí đồng vị
=> EA//BF
=> đpcm
P/s: Mệt quá O.O''

1) áp dụng định lí pytago vào tam giác DEF ta được:
EF2=DE2+DF2
=92+122
=225
=>EF=15(cm)
2)ta có \(DK=\frac{EF}{2}=\frac{15}{2}=7,5\left(cm\right)\)(định lí : trong t/g vuông vuông đường trung tuyến ứng với cạnh huyền bằng nưa độ dài cạnh huyền)
3)ta có: DE<DF<EF(9cm <12cm <15cm )
=>góc DFE<góc DEF< góc EDF(Định lí)

c1: EF=5cm
c2: EF=\(5\sqrt{2}\)cm
c3: \(DF=\sqrt{119}cm\)
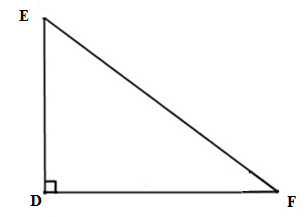
a) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=3^2+4^2\)
=> \(EF^2=9+16\)
=> \(EF^2=25\)
=> \(EF=5\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\left(cm\right).\)
b) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(EF^2=5^2+5^2\)
=> \(EF^2=25+25\)
=> \(EF^2=50\)
=> \(EF=\sqrt{50}\)
=> \(EF=5\sqrt{2}\left(cm\right)\) (vì \(EF>0\)).
Vậy \(EF=5\sqrt{2}\left(cm\right).\)
c) Xét \(\Delta EDF\) vuông tại \(D\left(gt\right)\) có:
\(EF^2=DE^2+DF^2\) (định lí Py - ta - go).
=> \(12^2=5^2+DF^2\)
=> \(DF^2=12^2-5^2\)
=> \(DF^2=144-25\)
=> \(DF^2=119\)
=> \(DF=\sqrt{119}\left(cm\right)\) (vì \(DF>0\)).
Vậy \(DF=\sqrt{119}\left(cm\right).\)
Chúc bạn học tốt!

b. Ta co goc EMD + goc EMH =90 mà DEM = HEM nen EMD = EMH. Xet 2 tam giac DEM va HEM có EH canh chung, goc EMH =EMD, DEM=HEM
C. EF=EK suy ra tam giac EFK can tai E. EM la tia phan giác, cung là đường cao, ta lại có ED vuong góc voi EK. Suy ra M là trực tâm. Mà MH vuong goc EF. Suy ra KMH thang hang

Theo định lí Pytago cho tam giác DEF vuông tại D
EF = \(\sqrt{DE^2+DF^2}=\sqrt{10^2+24^2}=26\)cm